题目内容
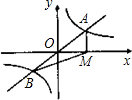 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=| k | x |
分析:根据△ABM的面积可得点A的横纵坐标的积,进而可得k的值.
解答:解:设点A的坐标为(x,y),
∴B的坐标为(-x,-y),
∵S△ABM=4,
∴
×2x×y=4,
∴xy=4,
∴k=xy=4,
故答案为4.
∴B的坐标为(-x,-y),
∵S△ABM=4,
∴
| 1 |
| 2 |
∴xy=4,
∴k=xy=4,
故答案为4.
点评:考查反比例函数与一次函数的交点问题;用到的知识点为:反比例函数的比例系数等于在它上面的点的横纵坐标的积.

练习册系列答案
相关题目
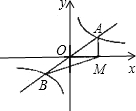 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=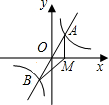 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=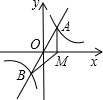 如图,直线y=mx与双曲线
如图,直线y=mx与双曲线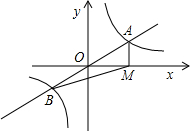 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=