题目内容
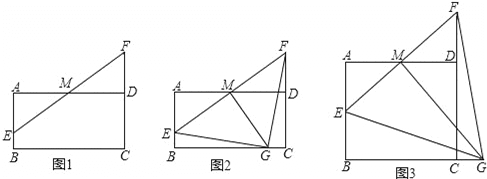
【题目】如图,在矩形![]() 中,
中, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,且点
,且点![]() 在矩形
在矩形![]() 内部,再延长
内部,再延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证: A、G、D三点在以点E为圆心,EA的长为半径的圆上;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
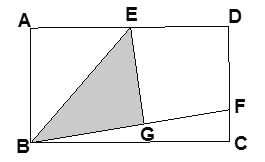
【答案】(1)证明见解析 ;
(2)![]() ;(3)
;(3) ![]()
【解析】【试题分析】(1)根据![]() 是
是![]() 的中点,得AE=DE;
的中点,得AE=DE; ![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,
,
得AE=EG ,则 AE=DE= EG,即证;
(2)连接![]() ,(图形见解析)则
,(图形见解析)则![]() ,
, ![]() .得
.得![]() 根据全都能三角形对应边相等,得
根据全都能三角形对应边相等,得![]() ;设
;设![]() ,
, ![]() ,则有
,则有![]() ,
, ![]() ,由折叠得
,由折叠得![]() ,
, ![]() . 在
. 在![]() 中,
中, ![]() ,
,
即![]() ,解得a、b之间的关系:
,解得a、b之间的关系: ![]() ,即
,即 ![]()
得: ![]() .
.
(3)思路同(2),![]() .设
.设![]()
![]()
由![]() 得
得![]() ,
, ![]() .
. ![]() . 在
. 在![]() 列勾股定理方程,得
列勾股定理方程,得![]() ,即
,即![]() .
. ![]()
![]() ,即求.
,即求.
【试题解析】
(1)∵![]() 是
是![]() 的中点
的中点
∴AE=DE
∵![]() 沿
沿![]() 折叠后得到
折叠后得到![]()
∴AE=EG
∴AE=DE= EG
∴三点A、G、D在以点E为圆心,EA的长为半径的圆上
(2)连接![]() ,
,
则![]() ,
, ![]() .
.
![]()
![]()
设![]() ,
, ![]() ,
,
则有![]() ,
, ![]() ,
,
由对称性有![]() ,
,
![]() .
.
在![]() ,
,
即![]() ,
,
![]() ,
,
∴![]()
![]()
![]()
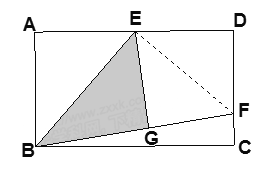
(3)由(2)知, ![]() .设
.设![]() ,则有
,则有![]()
∵![]()
![]() ,
, ![]() .
.
![]() .
.
在![]() 中,
中, ![]() ,
,
即![]() .
.
![]()
![]()

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】在九年级体育中考中,某校某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位:次/分):44,45,42,48,46,43,47,45.则这组数据的极差为( )
A.2
B.4
C.6
D.8
【题目】甲、乙、丙三位选手各10次射击成绩的平均数和方差,统计如下表:
选手 | 甲 | 乙 | 丙 |
平均数 | 9.3 | 9.3 | 9.3 |
方差 | 0.026 | 0.015 | 0.032 |
则射击成绩最稳定的选手是 . (填“甲”、“乙”、“丙”中的一个)