题目内容
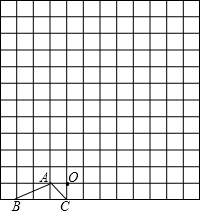 图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.(1)以点O为位似中心,在方格图中作出△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的位似比为1:2;
(2)△A1B1C1绕点B1顺时针旋转90°,画出旋转后得到的△A2B1C2,并求点A1在旋转过程中经过路线的长度.(结果保留π)
分析:(1)连接AO并延长,使OA1=2OA,则A1就是A的对应点,同法可以作出B,C的对应点,顺次连接各个对应点即可;
(2)将A1,B1,C1三点分别旋转90°,即可得到对应点,得到对应图形;
A1在旋转过程中经过路线是以B1为圆心,半径是B1A1的长,圆心角是90°的弧,根据弧长公式即可求解.
(2)将A1,B1,C1三点分别旋转90°,即可得到对应点,得到对应图形;
A1在旋转过程中经过路线是以B1为圆心,半径是B1A1的长,圆心角是90°的弧,根据弧长公式即可求解.
解答: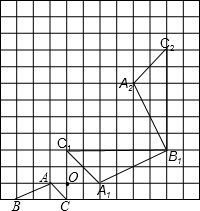 解:(1)作图如图(3分)
解:(1)作图如图(3分)
(2)作图如图(6分)
∵B1A1=
=2
(7分)
∴A1在旋转过程中经过路线的长度为:
π×2
=
π(8分)
 解:(1)作图如图(3分)
解:(1)作图如图(3分)(2)作图如图(6分)
∵B1A1=
| 22+42 |
| 5 |
∴A1在旋转过程中经过路线的长度为:
| 90 |
| 180 |
| 5 |
| 5 |
点评:本题主要考查了画位似图形以及弧长公式,画位似图形的一般步骤:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 18、如图,图中的小方格都是边长为1的正方形,△ABC与△A/B/C/是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
18、如图,图中的小方格都是边长为1的正方形,△ABC与△A/B/C/是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上. 21、如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上.
21、如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上. 21、如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A (0,-2)、B (3,-1)、C (2,1).
21、如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A (0,-2)、B (3,-1)、C (2,1).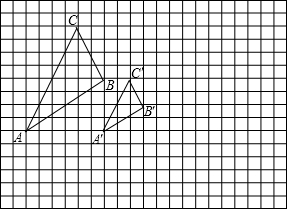 们的顶点都在小正方形的顶点上.
们的顶点都在小正方形的顶点上. 如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目
如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目