题目内容
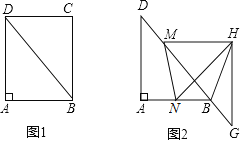
【题目】如图1在矩形ABCD中，AB＝6，BC＝8，△BCD沿BD的方向匀速平移得到△MGH，速度为1cm/s：同时点N从点B出发，沿BA方向匀速移动，速度为1cm/s，当点N停止移动时，△MGH也停止移动，如图2，设移动时间为t（0＜t＜6），连接MN，HB，HN
解答下列问题
（1）当t为何值时，MN∥HG？
（2）设四边形ADMN面积为y（cm2），求y和t之间的函数关系式；
（3）是否存在某一时刻t，使S△HBN：S四边形ADMN＝2：3？若存在，求出t值：若不存在，请说明理由；
（4）是否存在某一时刻t，使MN＝HB？若存在，求出t值；若不存在，请说明理由．
【答案】（1）
；（2）
；（3）t＝4，t＝6（不合题意舍去）；（4）
【解析】
（1）由勾股定理可求BD=10，通过证明△BAD∽△BNM，可得
，即可求t的值；
（2）过点M作ME⊥AB于点E，由相似三角形性质可得ME=
(10t)，由S四边形ADMN=S△ABD-S△BMN，可得y和t之间的函数关系式；
（3）由S△HBN：S四边形ADMN=2：3，可得t2-10t+24=0，即可求t的值；
（4）延长AB交HG于点F，由“HL”可证Rt△MNE≌Rt△HBF，可得BF=EN，即可求t的值．
（1）∵四边形ABCD是矩形
∴AB＝CD＝6，BC＝AD＝8，∠A＝90°
∴BD＝
＝10
由平移的性质可得：AD∥HG，且NM∥HG
∴MN∥AD
∴△BAD∽△BNM
∴
∴
∴；
（2）如图，过点M作ME⊥AB于点E，
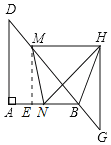
则ME∥AD
∴△BME∽△BDA
∴
∴ME= (10t)，
∵S四边形ADMN＝S△ABD﹣S△BMN，
∴y＝24﹣
，（0＜t＜6）
（3）∵S△HBN：S四边形ADMN＝2：3
∴
∴t2﹣10t+24＝0
∴t＝4，t＝6（不合题意舍去）
（4）如图，延长AB交HG于点F，
∵BA∥MH
∴△BFG∽△MHG
∴
∴BF＝
∵△BME∽△BDA
∴
∴BE＝
∴EN＝BE﹣BN＝6﹣
t，
∵ME＝HF，MN＝BH
∴Rt△MNE≌Rt△HBF（HL）
∴BF＝EN
∴
t＝6﹣t，
∴t＝
.
【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
（Ⅰ）写出
的值；
（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．
