题目内容
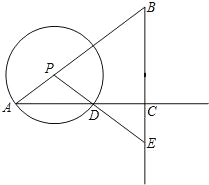
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,tanB=![]() ,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,设PA=x.
,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,设PA=x.
(1)当⊙P与BC相切时,求x的值;
(2)设CE=y,求y关于x的函数关系式,并写出x的取值范围.
【答案】(1)![]() ;(2)y=6﹣
;(2)y=6﹣![]() x(0≤x≤5).
x(0≤x≤5).
【解析】
试题分析:(1)首先利用∠ACB=90°,AC=8,tanB=![]() 得到BC=6,AB=10,然后利用⊙P与BC相切于点M时得到PM⊥BC,设PA=x.则PB=10-x,PM=PA=x,然后利用平行线分线段成比例定理
得到BC=6,AB=10,然后利用⊙P与BC相切于点M时得到PM⊥BC,设PA=x.则PB=10-x,PM=PA=x,然后利用平行线分线段成比例定理![]() 得到,从而求得答案;(2)过点P作PH⊥AD,垂足为点H,利用已知条件以及勾股定理可分别得到PH,AH,AD,CD的长,再由PH∥BE,可得
得到,从而求得答案;(2)过点P作PH⊥AD,垂足为点H,利用已知条件以及勾股定理可分别得到PH,AH,AD,CD的长,再由PH∥BE,可得![]() ,所以
,所以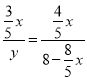 ,进而可求出y关于x的函数关系式;
,进而可求出y关于x的函数关系式;
试题解析:(1)∵∠ACB=90°,AC=8,tanB=![]() ,∴BC=6,AB=10,当⊙P与BC相切于点M时,PM⊥BC,因为PA=x,所以PM=PA=x,∵PM∥AC,∴
,∴BC=6,AB=10,当⊙P与BC相切于点M时,PM⊥BC,因为PA=x,所以PM=PA=x,∵PM∥AC,∴![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ;(2)如图:过点P作PH⊥AD,垂足为点H,
;(2)如图:过点P作PH⊥AD,垂足为点H,

∵∠ACB=90°,tanB=![]() ,∴sinA=
,∴sinA=![]() ,∵PA=x,∴PH=
,∵PA=x,∴PH=![]() x,∵∠PHA=90°,∴PH2+AH2=PA2,∴HA=
x,∵∠PHA=90°,∴PH2+AH2=PA2,∴HA=![]() x,∵在⊙P中,PH⊥AD,∴DH=AH=
x,∵在⊙P中,PH⊥AD,∴DH=AH=![]() x,∴AD=
x,∴AD=![]() x,又∵AC=8,∴CD=8﹣
x,又∵AC=8,∴CD=8﹣![]() x,∵∠PHA=∠BCA=90°,∴PH∥BE,∴
x,∵∠PHA=∠BCA=90°,∴PH∥BE,∴![]() ,∴
,∴ ,整理得:y=6﹣
,整理得:y=6﹣![]() x,由题意可得0≤x≤5.所以y=6﹣
x,由题意可得0≤x≤5.所以y=6﹣![]() x(0≤x≤5).
x(0≤x≤5).

练习册系列答案
相关题目