题目内容
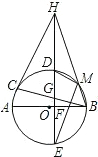
如图,AB为⊙O的直径,BC⊥AB,CP切⊙O于点P,连OC,交⊙O于N,交BP于E,连BN,AP.
(1)求证:BN平分∠PBC.
(2)连AC交BP于M,若AB=BC=4,求tan∠PAC的值.

(1)求证:BN平分∠PBC.
(2)连AC交BP于M,若AB=BC=4,求tan∠PAC的值.

(1)证明:连接PO,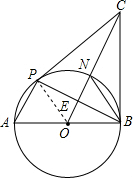
∵CB⊥AB,
∴CB是⊙O切线,
∵CP是⊙O切线,
∴PC=BC,
即C在PB垂直平分线上,
∵OP=OB,
∴O在PB的垂直平分线上,
∴OC⊥PB,PE=BE,
∴∠BEC=∠CBO=90°,
∴∠NBE+∠ENB=90°,∠CBN+∠NBO=90°,
∵ON=OB,
∴∠ONB=∠OBN,
∴∠NBP=∠NBC,
∴BN平分∠PBC.
(2)∵BE⊥OC,
∴∠OEB=∠CEB=∠OBC=90°,
∴∠OBE+∠EOB=90°,∠EBO+∠EBC=90°,
∴∠EOB=∠EBC,
∴△OEB∽△BEC,
∴
=
=
,
∵OB=
AB=2,BC=4,
∴BE=2OE,CE=2BE=4OE,
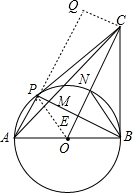 设OE=x,则CE=4x,
设OE=x,则CE=4x,
∵PE=BE,AO=OB,
∴AP=2OE=2x,
过C作CQ⊥AP交AP延长线于Q,
则∠Q=∠QPE=∠PEC=90°,
∴四边形QPEC是矩形,
∴QC=PE=BE=2x,QP=CE=4x,
∴AQ=4x+2x=6x,
在Rt△AQC中,tan∠PAC=
=
=
.

∵CB⊥AB,
∴CB是⊙O切线,
∵CP是⊙O切线,
∴PC=BC,
即C在PB垂直平分线上,
∵OP=OB,
∴O在PB的垂直平分线上,
∴OC⊥PB,PE=BE,
∴∠BEC=∠CBO=90°,
∴∠NBE+∠ENB=90°,∠CBN+∠NBO=90°,
∵ON=OB,
∴∠ONB=∠OBN,
∴∠NBP=∠NBC,
∴BN平分∠PBC.
(2)∵BE⊥OC,
∴∠OEB=∠CEB=∠OBC=90°,
∴∠OBE+∠EOB=90°,∠EBO+∠EBC=90°,
∴∠EOB=∠EBC,
∴△OEB∽△BEC,
∴
| OB |
| BC |
| OE |
| BE |
| BE |
| CE |
∵OB=
| 1 |
| 2 |
∴BE=2OE,CE=2BE=4OE,
 设OE=x,则CE=4x,
设OE=x,则CE=4x,∵PE=BE,AO=OB,
∴AP=2OE=2x,
过C作CQ⊥AP交AP延长线于Q,
则∠Q=∠QPE=∠PEC=90°,
∴四边形QPEC是矩形,
∴QC=PE=BE=2x,QP=CE=4x,
∴AQ=4x+2x=6x,
在Rt△AQC中,tan∠PAC=
| CQ |
| AQ |
| 2x |
| 6x |
| 1 |
| 3 |

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目

 写出自变量x的取值范围.
写出自变量x的取值范围.