题目内容
(2010•古冶区一模)阅读理解对于任意正实数a,b,∵
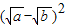 ≥0,∴a+b-2
≥0,∴a+b-2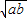 ≥0,∴a+b≥2
≥0,∴a+b≥2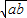 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.结论:在a+b≥2
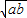 (a,b均为正实数)中,若ab为定值p,则a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2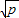 只有当a=b时,a+b有最小值2
只有当a=b时,a+b有最小值2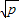 .
.根据上述内容,回答下列问题:
(1)若m>0,只有当m=______时,m+
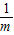 有最小值______.
有最小值______.(2)探索应用
如图,已知A(-2,0),B(0,-3),P为双曲线y=
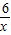 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.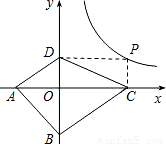
(3)实践应用
建筑一个容积为800m3,深为8m的长方体蓄水池,池壁每平方米造价为80元,池底每平方米造价为120元,如何设计池底的长、宽,使总造价最低?
【答案】分析:(1)根据题目给出的结论,可知当m=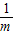 ,即m=1(m>0)时,m+
,即m=1(m>0)时,m+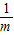 有最小值;
有最小值;
(2)若设P(x,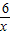 ),则S四边形ABCD=
),则S四边形ABCD= CA×DB=
CA×DB= (x+
(x+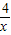 )+6,利用题目给出的结论,可知当x=
)+6,利用题目给出的结论,可知当x=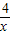 ,即x=2(x>0)时,S四边形ABCD有最小值,并求出各边长度,从而判断四边形ABCD的形状;
,即x=2(x>0)时,S四边形ABCD有最小值,并求出各边长度,从而判断四边形ABCD的形状;
(3)根据长方体的体积公式,可知此长方体蓄水池的底面积为100m2,如果设池底的一边为xm,那么另一边为(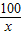 )m,根据长方体的表面积公式列出总造价y与x的函数关系式,再利用题目给出的结论,求出结果.
)m,根据长方体的表面积公式列出总造价y与x的函数关系式,再利用题目给出的结论,求出结果.
解答:解:(1)阅读理解:1(写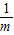 不扣分),2(2分)
不扣分),2(2分)
(2)探索应用:
设P(x, ),则C(x,0),D(0,
),则C(x,0),D(0,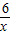 ),(4分)
),(4分)
∴CA=x+2,DB=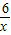 +3,(5分)
+3,(5分)
∴S四边形ABCD= CA×DB=
CA×DB= (x+2)(
(x+2)( +3)=
+3)= (x+
(x+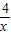 )+6(6分)
)+6(6分)
∵x>0∴x+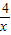 ≥2
≥2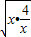 即x+
即x+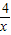 ≥4,∴x+
≥4,∴x+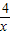 有最小值4,
有最小值4,
此时 (x+
(x+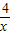 )+6有最小值12.
)+6有最小值12.
只有当x=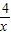 时,即x=2时,等号成立.
时,即x=2时,等号成立.
∴四边形ABCD面积的最小值为12.(7分)
此时,P(2,3),C(2,0),D(0,3),AB=BC=CD=DA= ,
,
∴四边形ABCD是菱形.(8分)
(3)实践应用:
设池底的一边为xm,另一边为(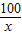 )m,
)m,
根据题意得y=80×2×(x+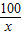 )×8+12000=1280(x+
)×8+12000=1280(x+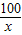 )+12000
)+12000
当x=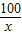 即x=10时,x+
即x=10时,x+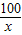 ≥2
≥2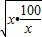 即x+
即x+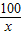 ≥20,
≥20,
此时x+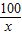 有最小值20,y有最小值37600元.
有最小值20,y有最小值37600元.
池底一边为10m时,使总造价最低.(10分)
点评:本题考查了学生的阅读理解能力与分析、解决实际问题的能力,是近几年中考的热点.透彻理解及灵活运用题目给出的结论是解决本题的关键.
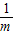 ,即m=1(m>0)时,m+
,即m=1(m>0)时,m+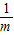 有最小值;
有最小值;(2)若设P(x,
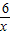 ),则S四边形ABCD=
),则S四边形ABCD= CA×DB=
CA×DB= (x+
(x+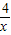 )+6,利用题目给出的结论,可知当x=
)+6,利用题目给出的结论,可知当x=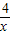 ,即x=2(x>0)时,S四边形ABCD有最小值,并求出各边长度,从而判断四边形ABCD的形状;
,即x=2(x>0)时,S四边形ABCD有最小值,并求出各边长度,从而判断四边形ABCD的形状;(3)根据长方体的体积公式,可知此长方体蓄水池的底面积为100m2,如果设池底的一边为xm,那么另一边为(
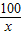 )m,根据长方体的表面积公式列出总造价y与x的函数关系式,再利用题目给出的结论,求出结果.
)m,根据长方体的表面积公式列出总造价y与x的函数关系式,再利用题目给出的结论,求出结果.解答:解:(1)阅读理解:1(写
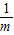 不扣分),2(2分)
不扣分),2(2分)(2)探索应用:
设P(x,
 ),则C(x,0),D(0,
),则C(x,0),D(0,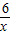 ),(4分)
),(4分)∴CA=x+2,DB=
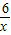 +3,(5分)
+3,(5分)∴S四边形ABCD=
 CA×DB=
CA×DB= (x+2)(
(x+2)( +3)=
+3)= (x+
(x+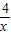 )+6(6分)
)+6(6分)∵x>0∴x+
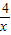 ≥2
≥2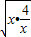 即x+
即x+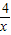 ≥4,∴x+
≥4,∴x+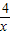 有最小值4,
有最小值4,此时
 (x+
(x+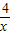 )+6有最小值12.
)+6有最小值12.只有当x=
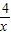 时,即x=2时,等号成立.
时,即x=2时,等号成立.∴四边形ABCD面积的最小值为12.(7分)
此时,P(2,3),C(2,0),D(0,3),AB=BC=CD=DA=
 ,
,∴四边形ABCD是菱形.(8分)
(3)实践应用:
设池底的一边为xm,另一边为(
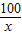 )m,
)m,根据题意得y=80×2×(x+
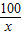 )×8+12000=1280(x+
)×8+12000=1280(x+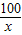 )+12000
)+12000当x=
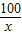 即x=10时,x+
即x=10时,x+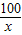 ≥2
≥2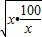 即x+
即x+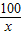 ≥20,
≥20,此时x+
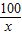 有最小值20,y有最小值37600元.
有最小值20,y有最小值37600元.池底一边为10m时,使总造价最低.(10分)
点评:本题考查了学生的阅读理解能力与分析、解决实际问题的能力,是近几年中考的热点.透彻理解及灵活运用题目给出的结论是解决本题的关键.

练习册系列答案
相关题目
(2010•古冶区一模)某男子排球队20名队员的身高如下表:
则此男子排球队20名队员的身高的众数是 cm.
| 身高(cm) | 180 | 186 | 188 | 192 | 193 |
| 人数(个) | 4 | 6 | 5 | 3 | 2 |
 nx-2m是否也经过点P?请说明理由;
nx-2m是否也经过点P?请说明理由;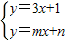 ,请你直接写出它的解;
,请你直接写出它的解;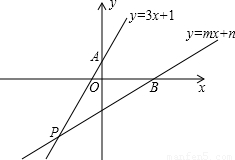
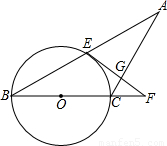
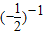 +|
+|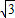 -2|-sin60°
-2|-sin60°