题目内容
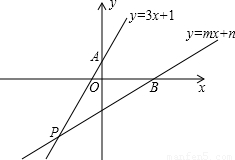
(2010•古冶区一模)如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:(1)求a的值,判断直线l3:y=-
 nx-2m是否也经过点P?请说明理由;
nx-2m是否也经过点P?请说明理由;(2)不解关于x,y的方程组
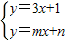 ,请你直接写出它的解;
,请你直接写出它的解;(3)若直线l1,l2表示的两个一次函数都大于0,此时恰好x>3,求直线l2的函数解析式.
【答案】分析:(1)因为(-2,a)在直线y=3x+1上,可求出a=-5;由点P(-2,-5)在直线y=mx+n上,可得-2m+n=-5,将P点横坐标-2代入y=- nx-2m,得y=-
nx-2m,得y=- n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P;
n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P;
(2)因为直线y=3x+1直线y=mx+n交于点P,所以方程组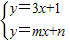 的解就是P点的坐标;
的解就是P点的坐标;
(3)因为直线l1,l2表示的两个一次函数都大于0,此时恰好x>3,所以直线l2过点(3,0),又有直线l2过点P(-2,-5),可得关于m、n的方程组,解方程组即可.
解答:解:(1)∵(-2,a)在直线y=3x+1上,
∴当x=-2时,a=-5(2分)
直线y=- nx-2m也经过点P,
nx-2m也经过点P,
∵点P(-2,-5)在直线y=mx+n上,
∴-2m+n=-5,
∴将P点横坐标-2代入y=- nx-2m,得y=-
nx-2m,得y=- n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P.(4分)
n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P.(4分)
(2)解为 .(6分)
.(6分)
(3)∵直线l1,l2表示的两个一次函数都大于0,此时恰好x>3
∴直线l2过点(3,0),(7分)
又∵直线l2过点P(-2,-5)
∴ 解得
解得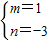 (8分)
(8分)
∴直线l2的函数解析式为y=x-3.(9分)
点评:用待定系数法确定函数的解析式,是常用的一种解题方法,另外本题还渗透了数形结合的思想,题出的比较好.
 nx-2m,得y=-
nx-2m,得y=- n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P;
n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P;(2)因为直线y=3x+1直线y=mx+n交于点P,所以方程组
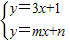 的解就是P点的坐标;
的解就是P点的坐标;(3)因为直线l1,l2表示的两个一次函数都大于0,此时恰好x>3,所以直线l2过点(3,0),又有直线l2过点P(-2,-5),可得关于m、n的方程组,解方程组即可.
解答:解:(1)∵(-2,a)在直线y=3x+1上,
∴当x=-2时,a=-5(2分)
直线y=-
 nx-2m也经过点P,
nx-2m也经过点P,∵点P(-2,-5)在直线y=mx+n上,
∴-2m+n=-5,
∴将P点横坐标-2代入y=-
 nx-2m,得y=-
nx-2m,得y=- n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P.(4分)
n×(-2)-2m=-2m+n=-5,这说明直线l3也经过点P.(4分)(2)解为
 .(6分)
.(6分)(3)∵直线l1,l2表示的两个一次函数都大于0,此时恰好x>3
∴直线l2过点(3,0),(7分)
又∵直线l2过点P(-2,-5)
∴
 解得
解得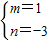 (8分)
(8分)∴直线l2的函数解析式为y=x-3.(9分)
点评:用待定系数法确定函数的解析式,是常用的一种解题方法,另外本题还渗透了数形结合的思想,题出的比较好.

练习册系列答案
相关题目
(2010•古冶区一模)某男子排球队20名队员的身高如下表:
则此男子排球队20名队员的身高的众数是 cm.
| 身高(cm) | 180 | 186 | 188 | 192 | 193 |
| 人数(个) | 4 | 6 | 5 | 3 | 2 |
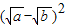 ≥0,∴a+b-2
≥0,∴a+b-2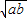 ≥0,∴a+b≥2
≥0,∴a+b≥2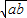 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.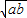 (a,b均为正实数)中,若ab为定值p,则a+b≥2
(a,b均为正实数)中,若ab为定值p,则a+b≥2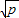 只有当a=b时,a+b有最小值2
只有当a=b时,a+b有最小值2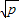 .
.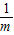 有最小值______.
有最小值______.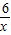 (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.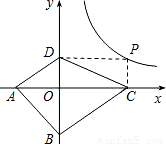
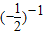 +|
+|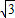 -2|-sin60°
-2|-sin60°