题目内容
【题目】我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
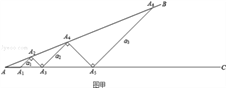
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能“或“不能”)
(2)设AA1=A1A2=A2A3=1.则θ= 度;
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
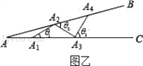
数学思考:
(3)若只能摆放5根小棒,求θ的范围.
【答案】(1)能.(2)θ=22.5度;(3) 15°≤θ<18°.
【解析】试题分析:(1)射线可无限延展,所以可以无限摆下去.(2)三角形AA1A2是等腰三角形,所以θ=22.5° .(3)根据三角形内角和定理和等腰三角形的性质列不等式可以得到.
试题解析:
(1)答: 能 .
(2)θ= 22.5 度;∠A1A2A3=45°.AA1=A1A2, , ![]() θ=22.5°.
θ=22.5°.
(3)∵A4A3=A4A5,
∴∠A4A3A5=∠A4A5A3=4θ°,
∵根据三角形内角和定理和等腰三角形的性质,
∴6θ≥90°,5θ<90°,
∴15°≤θ<18°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目