Question

【题目】如图，已知一次函数y1=（m﹣2）x+2与正比例函数y2=2x图象相交于点A（2，n），一次函数y1=（m﹣2）x+2与x轴交于点B．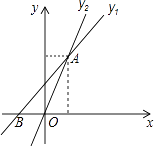

（1）求m、n的值；
（2）求△ABO的面积；
（3）观察图象，直接写出当x满足时，y1＞y2 ．

Answer 1

【答案】
（1）解：把点A（2，n）代入y2=2x得n=2×2=4，则A点坐标为（2，4），

把A（2，4）代入y1=（m﹣2）x+2得，4=（m﹣2）×2+2

解得m=3

（2）解：∵m=3，

∴y1=x+2，

令y=0，则x=﹣2，

∴B（﹣2，0），

∵A（2，4），

∴△ABO的面积= ×2×4=4

（3）x＜2
【解析】解：（3）由图象可知：当x＜2时，y1＞y2 ．
所以答案是x＜2．