题目内容
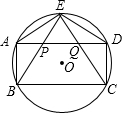 如图,凸五边形ABCDE内接于半径为1的⊙O,ABCD是矩形,AE=ED,且BE和CE把AD三等分.则此五边形ABCDE的面积是
如图,凸五边形ABCDE内接于半径为1的⊙O,ABCD是矩形,AE=ED,且BE和CE把AD三等分.则此五边形ABCDE的面积是
- A.

- B.

- C.

- D.
D
分析:可过点E作EH⊥AD,交圆O与H,设EF=h,由相交弦定理结合平行线分线段成比例可得AF的长,将五边形的面积简化为一个四边形与三角形的和,进而求解其和即可.
解答:如图,作EH⊥AD,BC,F和G分别为EH与AD、BC的交点,H在圆周上,
∵AE=ED,EH⊥AD,
∴AF=DF,即直线EH是AD的垂直平分线,
∵矩形ABCD内接⊙O,
∴EH过O,

记EF=h,0<h<1,则FH=2-h,
由AF=FD及相交弦定理,得AF=FD= =
= ,
,
又FG=2-2h,
所以SABCDE=S矩形ABCD+S△AED
=(2-2h)•2 +
+ •h•2
•h•2
=(4-3h) ,
,
由题设知PQ= AD=
AD= BC,由PQ∥BC得EF=
BC,由PQ∥BC得EF= EG,即EF=
EG,即EF= FG,h=1-h,所以h=
FG,h=1-h,所以h= ,
,
故SABCDE=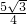 .
.
故选D.
点评:本题主要考查了平行线分线段成比例的性质以及圆形的相交弦定理问题,能够将所学四边形知识与圆联系起来,从而快速求解.
分析:可过点E作EH⊥AD,交圆O与H,设EF=h,由相交弦定理结合平行线分线段成比例可得AF的长,将五边形的面积简化为一个四边形与三角形的和,进而求解其和即可.
解答:如图,作EH⊥AD,BC,F和G分别为EH与AD、BC的交点,H在圆周上,
∵AE=ED,EH⊥AD,
∴AF=DF,即直线EH是AD的垂直平分线,
∵矩形ABCD内接⊙O,
∴EH过O,

记EF=h,0<h<1,则FH=2-h,
由AF=FD及相交弦定理,得AF=FD=
 =
= ,
,又FG=2-2h,
所以SABCDE=S矩形ABCD+S△AED
=(2-2h)•2
 +
+ •h•2
•h•2
=(4-3h)
 ,
,由题设知PQ=
 AD=
AD= BC,由PQ∥BC得EF=
BC,由PQ∥BC得EF= EG,即EF=
EG,即EF= FG,h=1-h,所以h=
FG,h=1-h,所以h= ,
,故SABCDE=
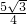 .
.故选D.
点评:本题主要考查了平行线分线段成比例的性质以及圆形的相交弦定理问题,能够将所学四边形知识与圆联系起来,从而快速求解.

练习册系列答案
相关题目
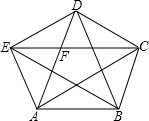 如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.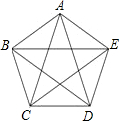 已知:如图,凸五边形ABCDE中,S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1,则S五边形ABCDE=
已知:如图,凸五边形ABCDE中,S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1,则S五边形ABCDE=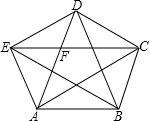 如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
