题目内容
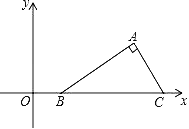
【题目】如图,在△ABC中,AB=AC,AD和CE是高,∠ACE=45°,点F是AC的中点,AD与FE,CE分别交于点G、H,∠BCE=∠CAD,有下列结论:①图中存在两个等腰直角三角形;②△AHE≌△CBE;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的个数有( )
AE2;④S△ABC=4S△ADF.其中正确的个数有( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
①图中有3个等腰直角三角形,故结论错误;
②根据ASA证明即可,结论正确;
③利用面积法证明即可,结论正确;
④利用三角形的中线的性质即可证明,结论正确.
∵CE⊥AB,∠ACE=45°,
∴△ACE是等腰直角三角形,
∵AF=CF,
∴EF=AF=CF,
∴△AEF,△EFC都是等腰直角三角形,
∴图中共有3个等腰直角三角形,故①错误,
∵∠AHE+∠EAH=90°,∠DHC+∠BCE=90°,∠AHE=∠DHC,
∴∠EAH=∠BCE,
∵AE=EC,∠AEH=∠CEB=90°,
∴△AHE≌△CBE,故②正确,
∵S△ABC=![]() BCAD=
BCAD=![]() ABCE,AB=AC=
ABCE,AB=AC=![]() AE,AE=CE,
AE,AE=CE,
∴BCAD=![]() CE2,故③正确,
CE2,故③正确,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴S△ABC=2S△ADC,
∵AF=FC,
∴S△ADC=2S△ADF,
∴S△ABC=4S△ADF.
故选C.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目