题目内容
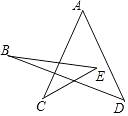
【题目】如图,△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F、E分别为AC、AD上两动点,连接CE、EF,则CE+EF的最小值为 . 
【答案】6
【解析】解:作F关于AD的对称点为M,作AB边上的高CP,
∵AD平分∠CAB,△ABC为锐角三角形,
∴M必在AC上,
∵F关于AD的对称点为M,
∴ME=EF,
∴EF+EC=EM+EC,
即EM+EC=MC≥PC(垂线段最短),
∵△ABC的面积是30,AB=10,
∴ ![]() ×10×PC=30,
×10×PC=30,
∴PC=6,
即CE+EF的最小值为:6.
所以答案是:6.
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目