题目内容
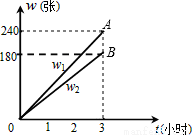
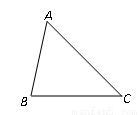
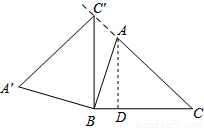
在锐角△ABC中，AB=5，BC=6，∠ACB=45°（如图）,将△ABC绕点B按逆时针方向旋转得到△A′BC′（顶点A、C分别与A′、C′对应），当点C′在线段CA的延长线上时，则AC′的长度为 .
.
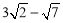【解析】
试题分析：如图：由旋转的性质可得：∠A′C′B=∠ACB=45°，BC=BC′，∴∠BC′C=∠ACB=45°.
∴∠CBC′=180°-∠BC′C-∠ACB=90°.
∵BC=6，∴
.
过点A作AD⊥BC于点D，
∵∠ACB=45°，∴△ACD是等腰直角三角形.
设AD=x，则CD=x，∴BD=BC-CD=6-x.
在△ABD中，AD2+BD2=AB2，
∴x2+（6-x）2=52，
解得：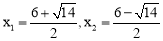
（不合题意舍去）.
∴
.
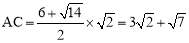∴AC′的长度为：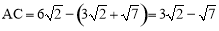
.
考点：1.旋转的性质；2．等腰直角三角形的判定和性质；3.勾股定理；4.解一元二次方程．
练习册系列答案
相关题目
