题目内容
【题目】等边三角形△ABC,直线1过点C且垂直AC.
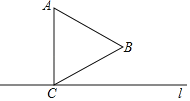
(1)请在直线1上作出点D,使得△ABD的周长最小.
(2)在(1)的条件下,连接AD,BD,求证,AD=2BD.
【答案】(1)见解析;(2)见解析
【解析】
(1)作点A关于直线l的对称点A′,连接AA′交直线1于点D,此时使得△ABD的周长最小.
(2)在(1)的条件下,连接AD,BD,根据对称性和30度角所对直角边等于斜边的一半即可证明AD=2BD.
解:(1)如图所示:

作点A关于直线l的对称点A′,连接AA′,与直线l交于点D,
则点D即为所求作的点.
(2)根据对称性可知:
AC=A′C,AD=A′D,
∵△ABC为等边三角形,
∴AC=BC=AB,∠ACB=60°=∠BAC,
∴A′C=BC,
∴∠A′=∠A′BC=30°,∠A′=∠DAA′=30°,
∴∠ABD=90°,
∴AD=2BD.

练习册系列答案
相关题目