Question

【题目】如图，在正方形ABCD中，动点P在射线CB上（与B、C不重合），连结AP，过D作DF∥AP交直线BC于点F，过F作FE⊥直线BD于点E，连结AE、PE．

（1）如图，当点P在线段CB上时

①求证：△ABP≌△DCF；

②点P在运动过程中，探究：△AEP的形状是否发生变化，若不变，请判断△AEP的形状，并说明理由；

（2）如图，当点P在CB的延长线上时,若正方形ABCD的边长为1，设BP＝x，当x为何值时，DF平分∠BDC？

Answer 1

【答案】(1)①证明见解析；②△AEP的形状不发生变化，△AEP是等腰直角三角形，理由见解析；（2）当x＝﹣1时，DF平分∠BDC．

【解析】

（1）①根据AAS即可证明△ABP≌△DCF；②连结CE，先证△ABE≌△CBE，证得EB＝EF，∠EBF＝∠EFB＝45°，再证得△EBP≌△EFC，得出AE＝EP∠AEB+∠BEP＝∠BEC+∠CEF＝90°，即可得出△AEP是等腰直角三角形；（2）若DF平分∠BDC，

则EF＝CF，故CF＝BP＝x，BF＝1﹣x，由△BEF是等腰直角三角形得BF＝EF，即1﹣x＝x，解得x＝﹣1，则可求解.

(1)①证明：∵四边形ABCD是正方形， ∴AB＝DC，∠ABC＝∠DCF＝90°，

∵DF∥AP， ∴∠APB＝∠DFC，

在△ABP和△DCF中，

，

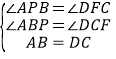∴△ABP≌△DCF；

②△AEP的形状不发生变化，△AEP是等腰直角三角形，

理由：连结CE，

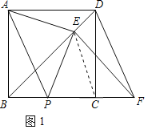
在△ABE和△CBE中，

，

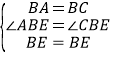∴△ABE≌△CBE，

∴AE＝CE，∠AEB＝∠CEB，

∵FE⊥BD，∠EBF＝45°，

∴EB＝EF，∠EBF＝∠EFB＝45°

∵△ABP≌△DCF，

∴BP＝FC，

∴△EBP≌△EFC，

∴EP＝EC，∠BEP＝∠FEC，

∴AE＝EP，

∠AEB+∠BEP＝∠BEC+∠CEF＝90°，

∴△AEP是等腰直角三角形；

（2）若DF平分∠BDC，

则EF＝CF，

∵CF＝BP＝x，

∴BF＝1﹣x，

∵△BEF是等腰直角三角形

∴BF＝EF，

∴1﹣x＝x，

解得x＝﹣1，

∴当x＝﹣1时，DF平分∠BDC．