题目内容
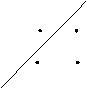
如图,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n的等式表示第n个正方形点阵中的规律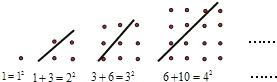
分析:直线上方点的个数为1+2+…+n-1,直线下方点的个数为:1+2+3+…+n-1+n,总的点的个数为n×n,由此可得正方形点阵的规律.
解答:解:根据分析得:直线上方点的个数为:1+2+…+n-1=
,
直线下方点的个数为:1+2+…+n=
,点的总个数为:n×n;
所以正方形点阵的规律为:
+
=n2.
| n(n-1) |
| 2 |
直线下方点的个数为:1+2+…+n=
| n(n+1) |
| 2 |
所以正方形点阵的规律为:
| n(n-1) |
| 2 |
| n(n+1) |
| 2 |
点评:本题是找规律型的题,直线将图象分成两个三角形,直线上方点的个数为1+2+…+n-1,直线下方点的个数为:1+2+…+n,而点的总个数为n2,直线上方点的个数加上直线下方点的个数等于总的点的个数.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
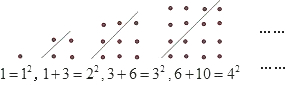
 26、如图,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n的等式表示第n个正方形点阵中的规律
26、如图,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n的等式表示第n个正方形点阵中的规律