题目内容
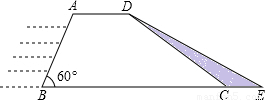
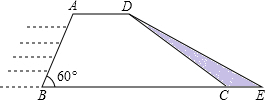
水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=600,背水坡面CD的长为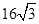 米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
已知需加固的大坝长为150米,求需要填土石方多少立方米?
求加固后的大坝背水坡面DE的坡度。

【答案】
解:(1)如图,分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G。
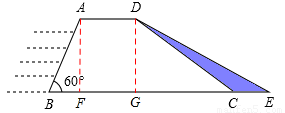
在Rt△ABF中,AB=16米,∠B=60°,
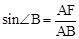 ,
,
∴ ,即DG=
,即DG=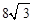 。
。
又∵CE=8,∴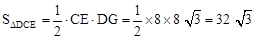 。
。
又∵需加固的大坝长为150,∴需要填方: 。
。
答:需要填土石方 立方米。
立方米。
(2)在Rt△DGC中,DC=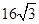 ,DG=
,DG=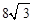 ,
,
∴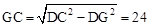 。∴GE=GC+CE=32。
。∴GE=GC+CE=32。
∴DE的坡度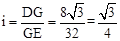 。
。
答:加固后的大坝背水坡面DE的坡度为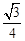 。
。
【解析】解直角三角形的应用(坡度坡角问题),锐角三角函数定义,特殊角的三角函数值,勾股定理。
【分析】(1)分别过A、D作下底的垂线,设垂足为F、G.在Rt△ABF中,已知坡面长和坡角的度数,可求得铅直高度AF的值,也就得到了DG的长;以CE为底,DG为高即可求出△CED的面积,再乘以大坝的长度,即为所需的填方体积。
(2)在Rt△CDG中,由勾股定理求CG的长,即可得到GE的长;Rt△DEG中,根据DG、GE的长即可求得坡角的正切值,即坡面DE的坡比。

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
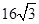 米,加固后大坝的横截面积为梯形ABED,CE的长为8米。
米,加固后大坝的横截面积为梯形ABED,CE的长为8米。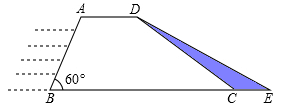
 .如图9所示,已知迎水坡面AB的长为16米,
.如图9所示,已知迎水坡面AB的长为16米,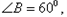 背水坡面
背水坡面 的长为
的长为 米,加固后大坝的横截面积为梯形
米,加固后大坝的横截面积为梯形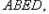
 的长为8米。
的长为8米。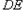 的坡度。
的坡度。
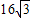 米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
米,加固后大坝的横截面积为梯形ABED,CE的长为8米.