Question

“5.12”汶川地震发生后，某天广安先后有两批自愿者救援队分别乘客车和出租车沿相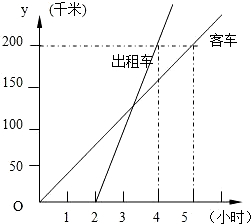同路线从广安赶往重灾区平武救援，下图表示其行驶过程中路程随时间的变化图象．
（1）根据图象，请分别写出客车和出租车行驶过程中路程与时间之间的函数关系式（不写出自变量的取值范围）；
（2）写出客车和出租车行驶的速度分别是多少；
（3）试求出出租车出发后多长时间赶上客车．

Answer 1

解：（1）根据直线过（0，0）、（5，200）两点，设解析式为：y=kx，
代入求出即可：k=40，
客车行驶过程中路程与时间之间的函数关系式为：y=40x，
出租车行驶过程中路程与时间之间的函数关系式为：y=100（x-2）；

（2）当客车走了5小时后，路程y=200，故客车行驶的速度为40千米/时，
当出租车走了（4-2）小时之后，路程y=200，故出租车行驶的速度为100千米/时；

（3）由题意得：40x=100x-200，
解得x=3．
∴x-2=．
答：当出租车出发小时赶上客车．
分析：（1）由图，已知与客车相关的直线过（0，0）、（5，200）两点，可根据待定系数法列方程，求函数关系式．再利用平移规律与出租车相关的直线的解析式；
（2）根据速度计算公式可以求出客车与出租车的速度；
（3）出租车赶上客车的时刻就是两直线交点的横坐标．
点评：本题主要考查用待定系数法求一次函数关系式，并会用一次函数研究实际问题，具备在直角坐标系中的读图能力．