题目内容
【题目】如图,直线![]() 的表达式为:
的表达式为:![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() ,
,![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() .
.
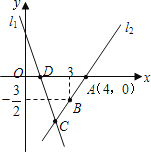
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)直接写出点![]() 的坐标________;
的坐标________;
(3)如果点![]() 在直线
在直线![]() 上,满足
上,满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(4)把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,当
的位置,当![]() 取得最小值时,直接写出
取得最小值时,直接写出![]() 的值
的值![]() ________.
________.
【答案】(1)y=![]() x6;(2)(2,3);(3)(6,3)或(2,3);(4)
x6;(2)(2,3);(3)(6,3)或(2,3);(4)![]()
【解析】
(1)根据待定系数法可求直线l2的表达式;
(2)联立直线l1与l2的表达式,解方程组即可得到结论;
(3)根据直线l1的解析式y=-3x+3求得D(1,0),设P(m,![]() m-6),根据S△ADP=2S△ADB,列方程即可得到结论;
m-6),根据S△ADP=2S△ADB,列方程即可得到结论;
(4)“把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,使
的位置,使![]() 取得最小值”等价为“
取得最小值”等价为“![]() 不动,点E沿直线y=3向右移动m个单位,使
不动,点E沿直线y=3向右移动m个单位,使![]() 取得最小值”,求出点A关于直线y=3的对称点A′的坐标,从而求出直线A′D的解析式,进而求出E′的坐标,即可求解.
取得最小值”,求出点A关于直线y=3的对称点A′的坐标,从而求出直线A′D的解析式,进而求出E′的坐标,即可求解.
(1)设直线l2的表达式为:y=kx+b,
∵直线l2经过点A(4,0),B(3,![]() ),
),
∴ ,解得:
,解得: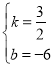 ,
,
∴直线l2的表达式为:y=![]() x6;
x6;
(2)联立可得方程组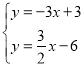 ,解得:
,解得: ![]() ,
,
∴C(2,3),
故答案是:(2,3);
(3)∵直线l1:y=3x+3与x轴交于点D,
∴D(1,0),
∵点![]() 在直线
在直线![]() 上,
上,
∴设P(m,![]() m6),
m6),
∵S△ADP=2S△ADB,
∴![]() ×3|
×3|![]() m6|=2×
m6|=2×![]() ×3×
×3×![]() ,
,
∴m=6或2,
∴点P的坐标(6,3)或(2,3);
(4)由题意得:E(0,3),
“把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,
的位置,![]() 取得最小值”等价为“
取得最小值”等价为“![]() 不动,点E沿直线y=3向右移动m个单位,
不动,点E沿直线y=3向右移动m个单位,![]() 取得最小值”,
取得最小值”,
作点A关于直线y=3的对称点A′,连接A′D,交直线y=3于点E′,此时,![]() 取得最小值,
取得最小值,
∵A(4,0),
∴A′(4,6),
设直线A′D的解析式为:y=kx+b,
把A′(4,6),D(1,0)代入得:![]() ,解得:
,解得:![]() ,
,
∴直线A′D的解析式为:y=2x-2,
令y=3代入y=2x-2,解得:x=![]() ,即:E′(
,即:E′(![]() ,3),
,3),
∴m=![]() -0=
-0=![]() .
.
故答案是:![]() .
.


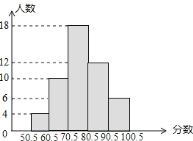
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.