题目内容
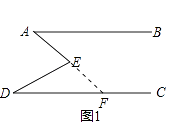
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED. 
(1)探究猜想: ①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
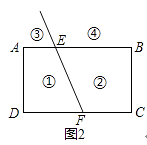
(2)拓展应用: 如图2,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).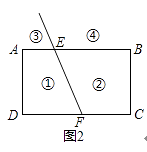
【答案】
(1)解:①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)解:根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
【解析】(1)①根据图形猜想得出所求角度数即可;②根据图形猜想得出所求角度数即可;③猜想得到三角关系,理由为:延长AE与DC交于F点,由AB与DC平行,利用两直线平行内错角相等得到一对角相等,再利用外角性质及等量代换即可得证;(2)分四个区域分别找出三个角关系即可.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目