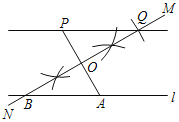
题目内容
【题目】如图，在每个小正方形的边长为1的网格中，
的顶点
均在格点上．
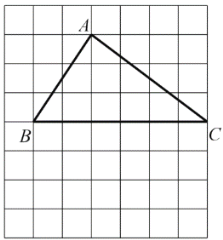
（Ⅰ）
的长等于__________；
（Ⅱ）请用无刻度的直尺，在如图所示的网格中，画出点
，点E在
上，且
，点F在上，使其满足
，并简要说明点的位置是如何找到的（不要求证明）______．
【答案】
取格点
且满足
连接
交
于
再取
关于对称的格点
，满足
延长
交
于
【解析】
（1）利用勾股定理直接计算即可；
（2）取格点且满足 连接可得答案，再取关于对称的格点，满足 延长与相交可得答案．
解：（1）由勾股定理得：
故答案为：
（2）取格点且满足 连接交
于
理由如下：由题意知：
所以点
即为所求作的点．
再取关于对称的格点，满足 延长交于
理由如下：
所以点
即为所求作的点．
故答案为：取格点且满足 连接交于再取关于对称的格点，满足 延长交于
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】2015年某省为加快建设综合交通体系，对铁路、公路、机场三个重大项目加大建设资金的投入．
（1）机场建设项目中所有6个机场投入的建设资金金额统计如下图，已知机场
投入的建设资金金额是机场
、
所投入建设资金金额之和的三分之二，求机场投入的建设资金金额是多少亿元？并补全条形统计图．
（2）将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表，根据扇形统计图及统计表中的信息，求得
；
；
；
；
．（请直接填写计算结果）
铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额（亿元） | |
投入资金（亿元） | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|
【题目】如图，P是弧AB所对弦AB上一动点，过点P作PM⊥AB交AB于点M，连接MB，过点P作PN⊥MB于点N.已知AB =6cm，设A 、P两点间的距离为xcm，P、N两点间的距离为ycm.（当点P与点A或点B重合时，y的值为0）
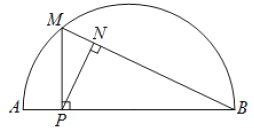
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
（说明：补全表格时相关数值保留一位小数）
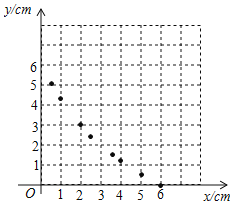
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象.
（3）结合画出的函数图象，解决问题：当△PAN为等腰三角形时，AP的长度约为____________cm.
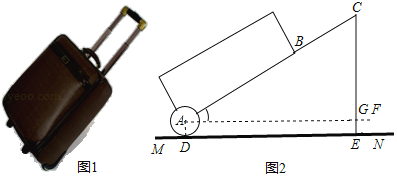
【题目】数学活动课上，张老师引导同学进行如下探究：如图1，将长为
的铅笔
斜靠在垂直于水平桌面
的直尺
的边沿上，一端
固定在桌面上，图2是示意图．
活动一
如图3，将铅笔绕端点顺时针旋转，与
交于点
，当旋转至水平位置时，铅笔的中点
与点
重合．
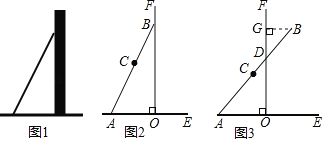
数学思考
（1）设
，点
到的距离
．
①用含
的代数式表示：
的长是_________
，
的长是________；
②
与的函数关系式是_____________，自变量的取值范围是____________．
活动二
（2）①列表：根据（1）中所求函数关系式计算并补全表格．
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点：根据表中数值，描出①中剩余的两个点
．
③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象．
数学思考
（3）请你结合函数的图象，写出该函数的两条性质或结论．
【题目】某学校初二和初三两个年级各有600名同学，为了科普卫生防疫知识，学校组织了一次在线知识竞赛，小宇分别从初二、初三两个年级随机抽取了40名同学的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．
．初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下（数据分成5组：
，
，
，
，
）：
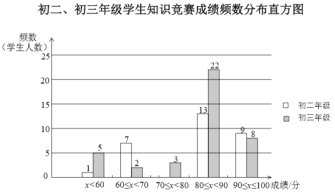
．初二年级学生知识竞赛成绩在这一组的数据如下：
80 80 81 83 83 84 84 85 86 87 88 89 89
．初二、初三学生知识竞赛成绩的平均数、中位数、方差如下：
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息，回答下列问题：
（1）补全上面的知识竞赛成绩频数分布直方图；
（2）写出表中
的值；
（3）
同学看到上述的信息后，说自己的成绩能在本年级排在前40%，
同学看到同学的成绩后说：“很遗憾，你的成绩在我们年级进不了前50%”．请判断
同学是________（填“初二”或“初三”）年级的学生，你判断的理由是________．
（4）若成绩在85分及以上为优秀，请估计初二年级竞赛成绩优秀的人数为____．
