题目内容
若b<0<a,则下列各式不成立的是
- A.a-b>0
- B.-a+b<0
- C.ab<0
- D.|a|>|b|
D
分析:根据不等式的基本性质和绝对值的定义进行判断.
解答:A、∵b<0<a,∴b<a,根据不等式的基本性质1可知,a-b>0,正确;
B、由A结合不等式的基本性质3,可知-a+b<0,正确;
C、∵b<0<a,根据不等式的基本性质2,可知ab<0,正确;
D、没法判定a、b的绝对值的大小,故本选项错误.
故选D.
点评:本题主要考查了不等式的基本性质和绝对值的性质.
不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
分析:根据不等式的基本性质和绝对值的定义进行判断.
解答:A、∵b<0<a,∴b<a,根据不等式的基本性质1可知,a-b>0,正确;
B、由A结合不等式的基本性质3,可知-a+b<0,正确;
C、∵b<0<a,根据不等式的基本性质2,可知ab<0,正确;
D、没法判定a、b的绝对值的大小,故本选项错误.
故选D.
点评:本题主要考查了不等式的基本性质和绝对值的性质.
不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
若a>b>0,则下列结论正确的是( )
| A、-a>-b | ||||
B、
| ||||
| C、a3<0 | ||||
| D、a2>b2 |
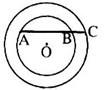 2、如图,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点C,若AB=4,BC=1,则下列整数于圆环面积最接近的是( )
2、如图,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点C,若AB=4,BC=1,则下列整数于圆环面积最接近的是( )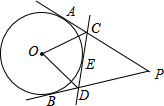 如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的个数为( )
如图,PA、PB、CD是⊙O的切线,A、B、E是切点,CD分别交PA、PB于C、D两点,若∠APB=40°,PA=5,则下列结论:①PA=PB=5;②△PCD的周长为5;③∠COD=70°.正确的个数为( )