题目内容
【题目】某班决定购买一些笔记本和文具盒做奖品.已知需要的笔记本数量是文具盒数量的3倍,购买的总费用不低于220元,但不高于250元.
(1)商店内笔记本的售价4元/本,文具盒的售价为10元/个,设购买笔记本的数量为x,按照班级所定的费用,有几种购买方案?每种方案中笔记本和文具盒数量各为多少?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)经过还价,老板同意4元/本的笔记本可打八折,10元/个的文具盒可打七折,用(2)中的最少费用最多还可以多买多少笔记本和文具盒?
【答案】(1)有两种购买方案:方案一:笔记本30本,文具盒10个;方案二:笔记本33本,文具盒11个;
(2)方案一的总费用最少,最少费用为220元;
(3)用(2)中的最少费用最多还可以多买9本笔记本和3个文具盒.
【解析】
(1)设笔记本的数量为x,根据题意列出不等式方程组.x取整数.
(2)根据(1)可求出答案.
(3)设用(2)中的最少费用最多还可以多买的文具盒的数量为y,列出不等式求解,y取整数.
(1)设笔记本的数量为x本,根据题意得:
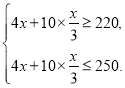
解得![]() .
.
∵x为正整数,
∴x可取30,31,32,33,34.
又∵![]() 也必须是整数,
也必须是整数,
∴![]() 可取10,11.
可取10,11.
∴有两种购买方案:
方案一:笔记本30本,文具盒10个;
方案二:笔记本33本,文具盒11个
(2)在(1)中,方案一购买的总数量最少,所以总费用最少.
最少费用为:4×30+10×10=220.
答:方案一的总费用最少,最少费用为220元.
(3)设用(2)中的最少费用最多还可以多买的文具盒数量为y,则笔记本数量为3y,
由题意得 4×80%(30+3y)+10×70%(10+y)≤220,
解得:![]() ,
,
∵y为正整数,
∴满足![]() 的最大正整数为3.
的最大正整数为3.
∴多买的笔记本为:3y=9(本).
答:用(2)中的最少费用最多还可以多买9本笔记本和3个文具盒.

 阅读快车系列答案
阅读快车系列答案