题目内容
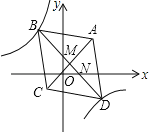
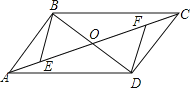
【题目】如图，ABCD的对角线AC、BD相交于点O，OE＝OF．
（1）求证：△BOE≌△DOF；
（2）若BD＝EF，连接DE、BF，判断四边形EBFD的形状，并说明理由．
【答案】（1）见解析；（2）四边形EBFD是矩形；理由见解析
【解析】
（1）由平行四边形的性质得出OB＝OD，由SAS证明△BOE≌△DOF即可；
（2）先证明四边形EBFD是平行四边形，再由对角线相等即可得出四边形EBFD是矩形．
（1）证明：∵四边形ABCD是平行四边形，
∴OB＝OD，
在△BOE和△DOF中，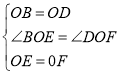
，
∴△BOE≌△DOF（SAS）；
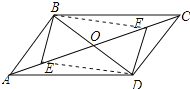
（2）解：四边形EBFD是矩形；理由如下：如图所示：
∵OB＝OD，OE＝OF，
∴四边形EBFD是平行四边形，
又∵BD＝EF，
∴四边形EBFD是矩形．
练习册系列答案
相关题目
【题目】为拓宽学生视野，我市某中学决定组织部分师生去庐山西海开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．为了安全，既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师．现有甲、乙两种大客车，它们的载客量和租金如表所示．
甲种客车 | 乙种客车 | |
载客量/（人/辆） | 30 | 42 |
租金/（元/辆） | 300 | 400 |
（1）参加此次研学旅行活动的老师和学生各有多少人？租用客车总数为多少辆？
（2）设租用x辆乙种客车，租车总费用为w元，请写出w与x之间的函数关系式；
（3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，租用乙种客车不少5辆，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．
