题目内容
【题目】若抛物线![]() (
(![]() 为常数)交
为常数)交![]() 轴于点
轴于点![]() ,与
,与![]() 轴的一个交点在2和3之间,顶点为
轴的一个交点在2和3之间,顶点为![]() .
.
①抛物线![]() 与直线
与直线![]() 有且只有一个交点;
有且只有一个交点;
②若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得的抛物线解析式为![]() ;
;
④点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中错误的是( )
A.①③B.②C.②④D.③④
【答案】C
【解析】
①将![]() 代入
代入![]() 可得一元二次方程,利用
可得一元二次方程,利用![]() 判断方程根的情况可知交点个数;②由
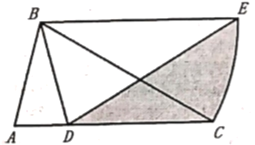
判断方程根的情况可知交点个数;②由![]() 可知抛物线的对称轴,再利用抛物线的增减性判断即可;③根据平移公式即可求出平移后的解析式;④BC边一定,只要其余三边和最小,周长就最小,因此可作点B关于y轴的对称点
可知抛物线的对称轴,再利用抛物线的增减性判断即可;③根据平移公式即可求出平移后的解析式;④BC边一定,只要其余三边和最小,周长就最小,因此可作点B关于y轴的对称点![]() ,作点C关于x轴的对称点
,作点C关于x轴的对称点![]() ,连接
,连接![]() ,交x轴、y轴与点D、点E,此时
,交x轴、y轴与点D、点E,此时![]() 长即为三边和的最小值.
长即为三边和的最小值.
解:①将![]() 代入
代入![]() 得
得![]() ,即
,即![]() ,
,![]() ,所以此方程有2个相等的实数根,即抛物线
,所以此方程有2个相等的实数根,即抛物线![]() 与直线
与直线![]() 有且只有一个交点,①正确; ②抛物线的对称轴为
有且只有一个交点,①正确; ②抛物线的对称轴为![]() ,所以点
,所以点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,
,![]() 当
当![]() 时,y随x的增大而增大,又
时,y随x的增大而增大,又![]() ,②错误;③将该抛物线向左平移2个单位,再向下平移2个单位得
,②错误;③将该抛物线向左平移2个单位,再向下平移2个单位得![]() ,化简得
,化简得![]() ,即
,即![]() ,③正确;④当
,③正确;④当![]() 时,抛物线的解析式为
时,抛物线的解析式为![]() ,
,![]() ,
,![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,又因为BC边一定,所以其余三边和的最小值即当点
,又因为BC边一定,所以其余三边和的最小值即当点![]() 在一条直线上时取最小值,作点B关于y轴的对称点
在一条直线上时取最小值,作点B关于y轴的对称点![]() ,作点C关于x轴的对称点
,作点C关于x轴的对称点![]() ,连接
,连接![]() ,其余三边和的最小值即为
,其余三边和的最小值即为![]() 长,
长,

由两点间距离公式可得![]() ,
,![]() ,所以四边形
,所以四边形![]() 周长的最小值为
周长的最小值为![]() ,④错误.综上所述,错误的有②④.
,④错误.综上所述,错误的有②④.
故选:C.

练习册系列答案
相关题目