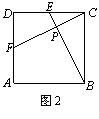
题目内容
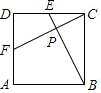 Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is
Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is分析:根据正方形的性质,可证明△CDF≌△BCE,因而能证明∠EPC是直角,利用正方形的边长可求出EB的长,再根据△EPC∽△ECB求出CP的长.
解答:解:∵四边形ABCD是正方形
∴△CDF≌△BCE
∴∠DFC=∠BEC
∵∠DFC+∠DCF=90°
∴∠BEC+∠DCF=90°
∴∠EPC=90°
∴△ECP∽△ECB,
∵BC=1,EC=
DC=
∴BE=
=
∵
=
∴
=
∴CP=
.
故答案为
.
∴△CDF≌△BCE
∴∠DFC=∠BEC
∵∠DFC+∠DCF=90°
∴∠BEC+∠DCF=90°
∴∠EPC=90°
∴△ECP∽△ECB,
∵BC=1,EC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=
12+(
|
| ||
| 2 |
∵
| BC |
| CP |
| BE |
| CE |
∴
| 1 |
| CP |
| ||||
|
∴CP=
| ||
| 5 |
故答案为
| ||
| 5 |
点评:本题考查了正方形的性质,全等三角形的判定和性质,以及相似三角形的判定和性质.

练习册系列答案
相关题目
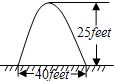 In the second (图形),suppose that arch(拱型门)is shaped like a parabola(抛物线).It is 40 feet wide at the base and 25 feet high.How wide the arch 16 feet above the ground?Answer:________feet.
In the second (图形),suppose that arch(拱型门)is shaped like a parabola(抛物线).It is 40 feet wide at the base and 25 feet high.How wide the arch 16 feet above the ground?Answer:________feet.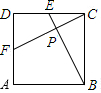 Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is________.(英汉词典:figure(缩写Fig.)图;length 长度;square 正方形;mid-point中点;intersect 相交;line segment 线段)
Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is________.(英汉词典:figure(缩写Fig.)图;length 长度;square 正方形;mid-point中点;intersect 相交;line segment 线段)