ЬтФПФкШн
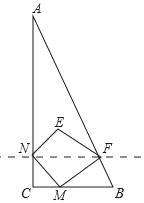
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯC=90ЁуЃЌЕуMДгЕуCГіЗЂбиCBЗНЯђвд1cm/sЕФЫйЖШдШЫйдЫЖЏЃЌЕНДяЕуBЭЃжЙдЫЖЏЃЌдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌЙ§ЕуMзїжБЯпMNНЛACгкЕуNЃЌЧвБЃГжЁЯNMC=45ЁуЃЎдйЙ§ЕуNзїACЕФДЙЯпНЛABгкЕуFЃЌСЌНгMFЃЌНЋЁїMNFЙигкжБЯпNFЖдГЦКѓЕУЕНЁїENFЃЎвбжЊAC=8cmЃЌBC=4cmЃЌЩшЕуMдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌЁїENFгыЁїANFжиЕўВПЗжЕФУцЛ§ЮЊyЃЈcm2ЃЉЃЎ
ЃЈ1ЃЉгУКЌtЕФДњЪ§ЪНБэЪОГіNCгыNFЃЛ
ЃЈ2ЃЉдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌФмЗёЪЙЕУЫФБпаЮMNEFЮЊе§ЗНаЮЃПШчЙћФмЃЌЧѓГіЯргІЕФtжЕЃЌШчЙћВЛФмЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЧѓyгыtЕФКЏЪ§ЙиЯЕЪНМАЯргІtЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉCN=tЃЌNF=![]() ЃЛЃЈ2ЃЉдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌФмЪЙЕУЫФБпаЮMNEFЮЊе§ЗНаЮЃЌtЕФжЕЮЊ
ЃЛЃЈ2ЃЉдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌФмЪЙЕУЫФБпаЮMNEFЮЊе§ЗНаЮЃЌtЕФжЕЮЊ![]() ЃЛЃЈ3ЃЉy=Љ
ЃЛЃЈ3ЃЉy=Љ![]() t2+2tЃЈ0ЃМtЁм2ЃЉЃЛy=
t2+2tЃЈ0ЃМtЁм2ЃЉЃЛy=![]() ЃЈ8ЉtЃЉ2ЃЈ2ЃМtЁм4ЃЉЃЛЃЎ
ЃЈ8ЉtЃЉ2ЃЈ2ЃМtЁм4ЃЉЃЛЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩжЊЃКCN=CM=tЃЌРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэ
ПЩЕУЃК![]() ЃЌгЩДЫМДПЩЧѓГіNFЃЛ
ЃЌгЩДЫМДПЩЧѓГіNFЃЛ
ЃЈ2ЃЉгЩвбжЊЕУГіCN=CM=tЃЌFNЁЮBCЃЌгЩЖдГЦЕФаджЪЕУГіЁЯENF=ЁЯMNF=ЁЯNMC=45ЁуЃЌ
MN=NEЃЌOE=OM=CN=tЃЌгЩе§ЗНаЮЕФаджЪЕУГі![]() ЃЌЕУГіЗНГЬЃЌНтЗНГЬ
ЃЌЕУГіЗНГЬЃЌНтЗНГЬ
МДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЃКЂйЕБ0ЃМtЁм2ЪБЃЌгЩШ§НЧаЮУцЛ§ЕУГі![]()
ЂкЕБ2ЃМtЁм4ЪБЃЌзїGHЁЭNFгкHЃЌгЩЃЈ1ЃЉЕУЃК![]() GH=NHЃЌGH=2FHЃЌЕУГі
GH=NHЃЌGH=2FHЃЌЕУГі
![]() гЩШ§НЧаЮУцЛ§ЕУГі
гЩШ§НЧаЮУцЛ§ЕУГі![]()
НтЃКЃЈ1ЃЉЁпЁЯC=90ЁуЃЌЁЯNMC=45ЁуЃЌ
ЁрCN=CM=tЃЌ
ЁпAC=8ЃЌ
ЁрAN=8ЉtЃЌ
ЁпNFЁЮBCЃЌ
Ёр![]()
Ёр![]()
Ёр![]()
ЃЈ2ЃЉФмЪЙЕУЫФБпаЮMNEFЮЊе§ЗНаЮЃЛРэгЩШчЯТЃК
СЌНгMEНЛNFгкOЃЌШчЭМ1ЫљЪОЃК
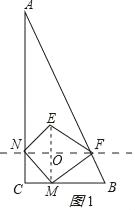
гЩЖдГЦЕФаджЪЕУЃКЁЯENF=ЁЯMNF=ЁЯNMC=45ЁуЃЌMN=NEЃЌOE=OM=CN=tЃЌ
ЁпЫФБпаЮMNEFЪЧе§ЗНаЮЃЌ
Ёр![]()
Ёр![]()
НтЕУЃК![]()
МДдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌФмЪЙЕУЫФБпаЮMNEFЮЊе§ЗНаЮЃЌtЕФжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЃК
ЂйЕБ0ЃМtЁм2ЪБЃЌ ![]()
МД![]()
ЂкЕБ2ЃМtЁм4ЪБЃЌШчЭМ2ЫљЪОЃКзїGHЁЭNFгкHЃЌ
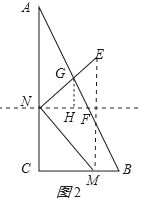
гЩЃЈ1ЃЉЕУЃК![]() GH=NHЃЌGH=2FHЃЌ
GH=NHЃЌGH=2FHЃЌ
Ёр![]()
Ёр![]()
МД![]()

 ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ
ОйвЛЗДШ§ЭЌВНЧЩНВОЋСЗЯЕСаД№АИ ПкЫугыгІгУЬтПЈЯЕСаД№АИ
ПкЫугыгІгУЬтПЈЯЕСаД№АИ УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ