题目内容
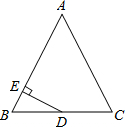（2012•盐城模拟）如图，△ABC中，AB=AC=13，BC=10，D为BC中点，DE⊥AB于E，则DE=| 60 |
| 13 |
| 60 |
| 13 |
分析：首先连接AD，由△ABC中，AB=AC=13，BC=10，D为BC中点，利用等腰三角形的三线合一的性质，即可证得：AD⊥BC，然后利用勾股定理，即可求得AD的长，又由DE⊥AB，利用有两角对应相等的三角形相似，可证得△BED∽△BDA，继而利用相似三角形的对应边成比例，即可求得DE的长．
解答：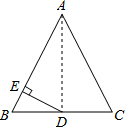
解：连接AD，
∵△ABC中，AB=AC=13，BC=10，D为BC中点，
∴AD⊥BC，BD=
BC=5，
∴AD=
=12，
∵DE⊥AB，
∴∠BED=∠BDA=90°，
∵∠B是公共角，
∴△BED∽△BDA，
∴
=
，
即
=
，
解得：DE=
．
故答案为：
．
解：连接AD，∵△ABC中，AB=AC=13，BC=10，D为BC中点，
∴AD⊥BC，BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
∵DE⊥AB，
∴∠BED=∠BDA=90°，
∵∠B是公共角，
∴△BED∽△BDA，
∴
| BD |
| AB |
| DE |
| AD |
即
| 5 |
| 13 |
| DE |
| 12 |
解得：DE=
| 60 |
| 13 |
故答案为：
| 60 |
| 13 |
点评：此题考查了相似三角形的判定与性质、等腰三角形的性质以及勾股定理．此题难度适中，解题的关键是准确作出辅助线，注意数形结合思想的应用．
练习册系列答案
相关题目
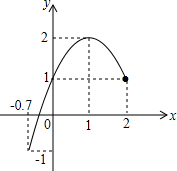（2012•盐城模拟）已知二次函数的图象（-0.7≤x≤2）如图所示、关于该函数在所给自变量x的取值范围内，下列说法正确的是（ ）
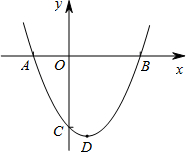（2012•盐城模拟）如图，已知抛物线y=ax2+bx+c（a≠0）与x轴相交于点A（-2，0）和点B，与y轴相交于点C，顶点D（1，-