题目内容
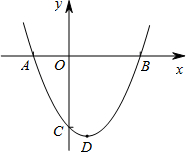 (2012•盐城模拟)如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(-2,0)和点B,与y轴相交于点C,顶点D(1,-
(2012•盐城模拟)如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(-2,0)和点B,与y轴相交于点C,顶点D(1,-| 9 | 2 |
(1)求抛物线对应的函数关系式;
(2)求四边形ACDB的面积;
(3)若平移(1)中的抛物线,使平移后的抛物线与坐标轴仅有两个交点,请直接写出一个平移后的抛物线的关系式.
分析:(1)根据题意设抛物线的解析式为顶点式方程y=a(x-1)2-
,然后利用待定系数法求抛物线的解析式即可;
(2)将四边形ACDB的面积分割成S△AOC+S△DOC+S△ODB,利用A,B,C,D的坐标求出面积即可;
(3)当抛物线与坐标轴仅有两个交点,即图象顶点在x轴上或经过原点时即符合要求,进而写出平移后的解析式即可.
| 9 |
| 2 |
(2)将四边形ACDB的面积分割成S△AOC+S△DOC+S△ODB,利用A,B,C,D的坐标求出面积即可;
(3)当抛物线与坐标轴仅有两个交点,即图象顶点在x轴上或经过原点时即符合要求,进而写出平移后的解析式即可.
解答: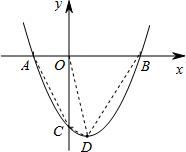 解:(1)设二次函数为y=a(x-1)2-
解:(1)设二次函数为y=a(x-1)2-
,
将点A(-2,0)代入上式得,
0=a(-2-1)2-
,
解得:a=
,
故y=
(x-1)2-
.
(2)令y=0,得0=
(x-1)2-
,
解得:x1=-2,x2=4,
则B(4,0),
令x=0,得y=-4,故C(0,-4),
S四边形ACDB=S△AOC+S△DOC+S△ODB,
=
×2×4+
×4×1+
×4×
,
=15,
故四边形ACDB的面积为15;
(3)如:向上平移
个单位,y=
(x-1)2;
或向上平移4个单位,y=
(x-1)2-
;
或向右平移2个单位,y=
(x-3)2-
;
或向左平移4个单位y=
(x+3)2-
(写出一种情况即可).
 解:(1)设二次函数为y=a(x-1)2-
解:(1)设二次函数为y=a(x-1)2-| 9 |
| 2 |
将点A(-2,0)代入上式得,
0=a(-2-1)2-
| 9 |
| 2 |
解得:a=
| 1 |
| 2 |
故y=
| 1 |
| 2 |
| 9 |
| 2 |
(2)令y=0,得0=
| 1 |
| 2 |
| 9 |
| 2 |
解得:x1=-2,x2=4,
则B(4,0),
令x=0,得y=-4,故C(0,-4),
S四边形ACDB=S△AOC+S△DOC+S△ODB,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
=15,
故四边形ACDB的面积为15;
(3)如:向上平移
| 9 |
| 2 |
| 1 |
| 2 |
或向上平移4个单位,y=
| 1 |
| 2 |
| 1 |
| 2 |
或向右平移2个单位,y=
| 1 |
| 2 |
| 9 |
| 2 |
或向左平移4个单位y=
| 1 |
| 2 |
| 9 |
| 2 |
点评:此题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来是解题关键.

练习册系列答案
相关题目
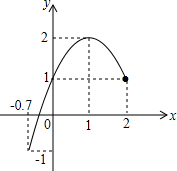 (2012•盐城模拟)已知二次函数的图象(-0.7≤x≤2)如图所示、关于该函数在所给自变量x的取值范围内,下列说法正确的是( )
(2012•盐城模拟)已知二次函数的图象(-0.7≤x≤2)如图所示、关于该函数在所给自变量x的取值范围内,下列说法正确的是( )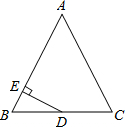 (2012•盐城模拟)如图,△ABC中,AB=AC=13,BC=10,D为BC中点,DE⊥AB于E,则DE=
(2012•盐城模拟)如图,△ABC中,AB=AC=13,BC=10,D为BC中点,DE⊥AB于E,则DE=