题目内容
已知y1=-x+2,y2=3x-4.
(1)当x分别取何值时,y1=y2,y1<y2,y1>y2?
(2)在同一坐标系中,分别作出这两个函数的图象,请你说说(1)中的解集与函数图象之间的关系.
(1)当x分别取何值时,y1=y2,y1<y2,y1>y2?
(2)在同一坐标系中,分别作出这两个函数的图象,请你说说(1)中的解集与函数图象之间的关系.
考点:一次函数与一元一次不等式
专题:
分析:(1)通过解方程、不等式来求x的取值范围;
(2)分别画出y1=-x+2,y2=3x-4的函数图象根据图象回答问题.
(2)分别画出y1=-x+2,y2=3x-4的函数图象根据图象回答问题.
解答:解:(1)当y1=y2时,-x+2=3x-4,解得,x=
;
当y1<y2时,-x+2<3x-4,解得,x>
;
当y1>y2时,-x+2>3x-4,解得,x<
;
(2)∵y1=-x+2,
∴当x=0时,y1=2.
当y1=0时,x=2.
∴该函数图象经过点(0,2),(2,0).
同理,函数y2=3x-4与坐标轴的交点是(0,-4),(
,0).
由(1)知,函数y1=-x+2与y2=3x-4的交点横坐标是
,则交点的纵坐标是y=-
+2=
,即交点坐标是(
,
).
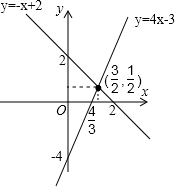
其图象如图所示:
 .
.
由图象可知:从函数的角度看,就是寻求使一次函数y1=-x+2的值等于(大于或小于)时一次函数y2=3x-4的值时自变量x的取值范围.
| 3 |
| 2 |
当y1<y2时,-x+2<3x-4,解得,x>
| 3 |
| 2 |
当y1>y2时,-x+2>3x-4,解得,x<
| 3 |
| 2 |
(2)∵y1=-x+2,
∴当x=0时,y1=2.
当y1=0时,x=2.
∴该函数图象经过点(0,2),(2,0).
同理,函数y2=3x-4与坐标轴的交点是(0,-4),(
| 4 |
| 3 |
由(1)知,函数y1=-x+2与y2=3x-4的交点横坐标是
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
其图象如图所示:
 .
.由图象可知:从函数的角度看,就是寻求使一次函数y1=-x+2的值等于(大于或小于)时一次函数y2=3x-4的值时自变量x的取值范围.
点评:本题考查了一次函数与一元一次不等式的关系.解题时,要“数形结合”,这样会使问题变得形象化,降低题的难度.

练习册系列答案
相关题目
如图,a,b,c三种物体的质量的大小关系是( )

| A、a>b>c |
| B、a>c>b |
| C、c>b>a |
| D、b>c>a |
如果□+2=0,那么“□”内应填的有理数是( )
| A、-2 | ||
B、-
| ||
C、±
| ||
D、
|
在四边形ABCD中,AB=CD,要使这个四边形是平行四边形,需添加的条件是( )
| A、AD∥BC |
| B、∠A=∠D |
| C、AB∥CD |
| D、∠A+∠B=180° |