题目内容
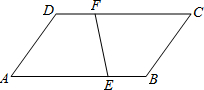
如图，已知在平行四边形ABCD中，点E、F分别在边AB、CD上，且AE=2EB，CF=2FD，连接EF．
（1）写出与
相等的向量______；
（2）填空
+
-
=______；
（3）求作：
-
．（保留作图痕迹，不要求写作法，请说明哪个向量是所求作的向量）
（1）写出与
| FC |
（2）填空
| AD |
| EB |
| EF |
（3）求作：
| AD |
| FE |
（1）在?ABCD中，AB∥CD，AB=CD，
∵AE=2EB，CF=2FD，
∴AE=
AB=
AB，
CF=
CD=
CD，
∴与
相等的向量是
；
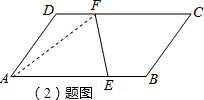
（2）如图，连接AF，
∵DF=CD-FC=
CD，
BE=AB-AE=
AB，
∴
=
，
∴
+
=
，
∵-
=
，
∴
-
=
+
=
，
又∵
=
，
∴
+
-
=
（或
）；
故答案为：（1）
；（2）
或
；
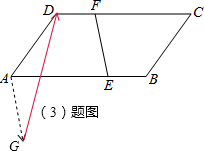
（3）如图，
即为所求作的
-
．
∵AE=2EB，CF=2FD，
∴AE=
| 2 |
| 1+2 |
| 2 |
| 3 |
CF=
| 2 |
| 1+2 |
| 2 |
| 3 |
∴与
| FC |
| AE |
（2）如图，连接AF，
∵DF=CD-FC=
| 1 |
| 3 |
BE=AB-AE=
| 1 |
| 3 |
∴
| EB |
| DF |
∴
| AD |
| EB |
| AF |
∵-
| EF |
| FE |
∴
| AF |
| EF |
| AF |
| FE |
| AE |
又∵
| AE |
| FC |
∴
| AD |
| EB |
| EF |
| AE |
| FC |
故答案为：（1）
| AE |
| AE |
| FC |
（3）如图，
| GD |
| AD |
| FE |
练习册系列答案
相关题目
、
、……、
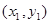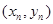都在直线
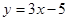上，若这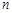
个点的横坐标的平均数为
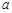，则这
