题目内容
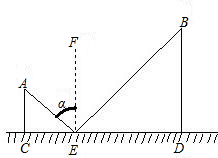如图，CD是平面镜，光线从A点出发经CD上点E反射照到B点，若入射角为α，AC⊥CD，BD⊥CD，且AC=3，BD=6，CD=12，则tanα值为分析：易证△ACE∽△BDE，可得CE的值．求∠A的正切值就是所求的∠α的正切值．
解答：解：∵∠AEC=∠BED，∠ACE=∠BDE，
∴△ACE∽△BDE，
∴AC：BD=CE：ED，
∴CE=4．
∵AC∥EF，
∴∠A=∠α．
∴tan∠A=tan∠α=CE：AC=
．
∴△ACE∽△BDE，
∴AC：BD=CE：ED，
∴CE=4．
∵AC∥EF，
∴∠A=∠α．
∴tan∠A=tan∠α=CE：AC=
| 4 |
| 3 |
点评：解决本题的关键是得到求得∠A的正切值就是所求的∠α的正切值，难点是利用相似三角形的判定与性质得到CE的值．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
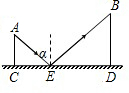如图，CD是平面镜，光线从A出发经CD上点E发射后照射到B点．若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=11，求tanα的值．
如图，CD是平面镜，光线从A点出发经CD上点E反射后照射到B点，若入射角为α（入射角等于反射角），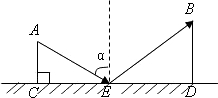
如图，CD是平面镜，光线从A点出发经CD上点E反射后照射到B点，若入射角α（入射角等于反射角），AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=11，则tanα=
如图，CD是平面镜，光线从A点出发经CD上点E反射照到B点，若入射角为α，AC⊥CD，BD⊥CD，且AC=3，BD=6，CD=12，则tanα值为（ ）