题目内容
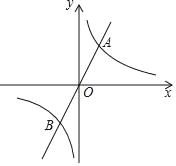
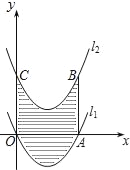
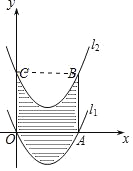
【题目】如图,已知抛物线l1:y=(x﹣2)2﹣4与x轴分别交于O、A两点,将抛物线l1向上平移得到l2,过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为12,则抛物线l2的函数表达式为( )
A. y=(x﹣2)2﹣1 B. y=(x﹣2)2+1 C. y=(x﹣2)2﹣2 D. y=(x﹣2)2+2
【答案】A
【解析】
根据题意和图象,可以由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积与矩形OABC的面积相等,从而可以解答本题.
解:∵抛物线l1:y=(x﹣2)2﹣4与x轴分别交于O、A两点,
∴当y=0时,得x1=0,x2=4,
∴点O(0,0),点B(4,0),
∴OB=4,
∵由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为12,连接BC,
∴矩形OABC的面积为12,
设OC=a,
∴4a=12,
解得,a=3,
∴抛物线l2的函数表达式为:y=(x﹣2)2﹣4+3=y=(x﹣2)2﹣1,
故选:A.

练习册系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.