题目内容
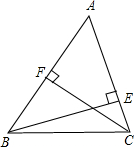 如图,已知BE、CF分别是△ABC的边AC、AB的高.
如图,已知BE、CF分别是△ABC的边AC、AB的高.
试说明:AC•BE=AB•CF.
证明:∵BE、CF分别是△ABC的边AC、AB的高,
∴∠AEB=∠AFC=90°,
又∵∠A=∠A,
∴△ABE∽△ACF,
∴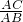 =
= ,
,
∴AC•BE=AB•CF.
或:∵BE、CF分别是△ABC的边AC、AB的高,
∴S△ABC= AC•BE=
AC•BE= AB•CF,
AB•CF,
∴AC•BE=AB•CF.
分析:利用两角对应相等,两三角形相似,证明△ABE与△ACF相似,再根据相似三角形对应边成比例列出比例式,然后转化成乘积式即可.
或利用三角形的面积列式整理即可得证.
点评:本题主要考查了相似三角形的判定与相似三角形的对应边成比例的性质,比较简单,准确识图是关键.
∴∠AEB=∠AFC=90°,
又∵∠A=∠A,
∴△ABE∽△ACF,
∴
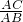 =
= ,
,∴AC•BE=AB•CF.
或:∵BE、CF分别是△ABC的边AC、AB的高,
∴S△ABC=
 AC•BE=
AC•BE= AB•CF,
AB•CF,∴AC•BE=AB•CF.
分析:利用两角对应相等,两三角形相似,证明△ABE与△ACF相似,再根据相似三角形对应边成比例列出比例式,然后转化成乘积式即可.
或利用三角形的面积列式整理即可得证.
点评:本题主要考查了相似三角形的判定与相似三角形的对应边成比例的性质,比较简单,准确识图是关键.

练习册系列答案
相关题目
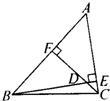 16、如图,已知BE和CF是△ABC的两条高,∠ABC=47°,∠ACB=82°,求∠FDB的度数.
16、如图,已知BE和CF是△ABC的两条高,∠ABC=47°,∠ACB=82°,求∠FDB的度数.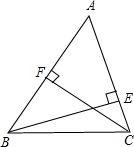 如图,已知BE、CF分别是△ABC的边AC、AB的高.
如图,已知BE、CF分别是△ABC的边AC、AB的高.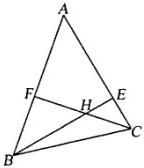 8、如图,已知BE,CF分别为△ABC的两条高,BE和CF相交于点H,若∠BAC=50°,则∠BHC为( )
8、如图,已知BE,CF分别为△ABC的两条高,BE和CF相交于点H,若∠BAC=50°,则∠BHC为( )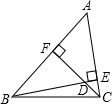 如图,已知BE和CF是△ABC的两条高,∠ABC=47°,∠ACB=82°,求∠FDB的度数.
如图,已知BE和CF是△ABC的两条高,∠ABC=47°,∠ACB=82°,求∠FDB的度数.