题目内容
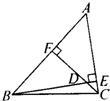16、如图，已知BE和CF是△ABC的两条高，∠ABC=47°，∠ACB=82°，求∠FDB的度数．分析：先根据三角形的内角和定理求得∠CBE和∠BCF的度数，再运用三角形外角的性质求得∠FDB的度数．
解答：解：∵BE和CF是△ABC的两条高，
∴∠BFC=90°，∠BEC=90°，
在△BFC和△BEC中，∠CBE=180°-∠BEC-∠ACB=8°，∠BCF=180°-∠BFC-∠ABC=43°，
∴∠FDB=∠CBE+∠BCF=51°．
∴∠BFC=90°，∠BEC=90°，
在△BFC和△BEC中，∠CBE=180°-∠BEC-∠ACB=8°，∠BCF=180°-∠BFC-∠ABC=43°，
∴∠FDB=∠CBE+∠BCF=51°．
点评：用到的知识点为：三角形一个外角等于和它不相邻的两个内角的和；三角形的内角和为180°．
练习册系列答案
相关题目
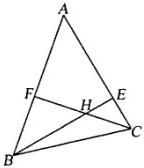8、如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为（ ）
如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC为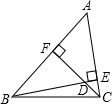
如图，已知BE和CF是△ABC的两条高，∠ABC=47°，∠ACB=82°，求∠FDB的度数．