题目内容
【题目】已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB_____.
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD_____.
∴∠MPF=∠PFD
∴∠_____+∠_____=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系:_____.




【答案】两直线平行,内错角相等如果两条直线都和第三条直线平行,那么这两条直线也互相平行∠EPM∠MPF∠EPF+∠PFD=∠PEB
【解析】
(1)根据对顶角相等可得∠BEF的度数,根据同旁内角互补,两直线平行,即可得出结论;
(2)①过点P作MN∥AB,根据平行线的性质得∠EPM=∠PEB,且有MN∥CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB+∠PFD.
②③的解题方法与①一样,分别过点P作MN∥AB,然后利用平行线的性质得到三个角之间的关系.
(1)∵∠1=120°,
∴∠BEF=120°,
又∵∠2=60°,
∴∠2+∠BEF=180°,
∴AB∥CD;
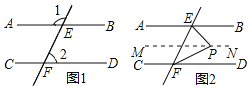
(2)①如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等).
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD(平行于同一条直线的两条直线互相平行).
∴∠MPF=∠PFD,
∴∠EPM+∠FPM=∠PEB+∠PFD(等式的性质),
即∠EPF=∠PEB+∠PFD,
故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;∠EPM,∠MPF;
②∠EPF+∠PEB+∠PFD=360°;
证明:如图3,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠BEP+∠EPM=180°,∠DFP+∠FPM=180°,
∴∠BEP+∠EPM+∠FPM+∠PFD=360°,
即∠EPF+∠PEB+∠PFD=360°;

③∠EPF+∠PFD=∠PEB.
理由:如图4,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠PEB=∠MPE,∠PFD=∠MPF,
∵∠EPF+∠FPM=∠MPE,
∴∠EPF+∠PFD=∠PEB.