题目内容
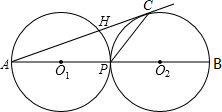 如图,外切于P点的⊙O1和⊙O2是半径为3cm的等圆,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )
如图,外切于P点的⊙O1和⊙O2是半径为3cm的等圆,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )A、2
| ||
B、3
| ||
| C、3cm | ||
| D、4.5cm |
分析:利用切线的概念,直径对的圆周角是直角,平行线的判定和性质,勾股定理求解.
解答:解:连接O2C,PH,AP是直径,
则∠AHP=90°,
由切线的概念知,∠O2CA=90°;
∴PH∥O2C,
由勾股定理得,AC=6
,
∵HP:O2C=AP:O2A,
∴HP=2,
由勾股定理得,AH=4
,HC=AC-AH=2
,
在直角三角形PHC中,由勾股定理得,PC=2
.
故选A.
则∠AHP=90°,
由切线的概念知,∠O2CA=90°;
∴PH∥O2C,
由勾股定理得,AC=6
| 2 |
∵HP:O2C=AP:O2A,
∴HP=2,
由勾股定理得,AH=4
| 2 |
| 2 |
在直角三角形PHC中,由勾股定理得,PC=2
| 3 |
故选A.
点评:本题考查了切线的性质和勾股定理的灵活运用.

练习册系列答案
相关题目
 如图,外切于P点的⊙O1和⊙O2的半径分别为2cm和4cm,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )
如图,外切于P点的⊙O1和⊙O2的半径分别为2cm和4cm,连心线交⊙O1于点A,交⊙O2于点B,AC与⊙O2相切于点C,连接PC,则PC的长为( )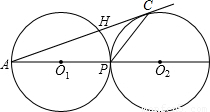
 cm
cm cm
cm
 cm
cm cm
cm
 cm
cm cm
cm