题目内容
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 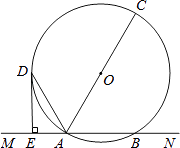
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
(3)在(2)的条件下,直接写出tan∠CAB的值.
【答案】
(1)证明:连接OD.
∵OA=OD
∴∠OAD=∠ODA
∵∠OAD=∠DAE
∴∠ODA∠DAE.
∴DO∥MN,
∵DE⊥MN,
∴∠ODE=∠DEM=90°
即OD⊥DE,
∵D在⊙O上
∴DE是⊙O的切线
(2)解:连接CD
∵∠AED=90°,DE=6,AE=3,
∴AD= ![]() =
= ![]() =3
=3 ![]() ,
,
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°,
∵∠CAD=∠DAE,
∴△ACD∽△ADE,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AC=15,
∴⊙O的半径是7.5cm
(3)解:作OF⊥MN于F,则四边形ODEF是矩形,OF=AD=6,
∴AF= ![]() =
= ![]() =4.5,
=4.5,
∴tan∠CAB= ![]() =
= ![]() =
= ![]() .
.
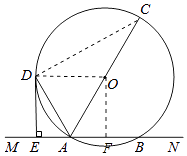
【解析】(1)连接OD欲证明DE是⊙O的切线,只要证明∠ODE=90°即可.(2)连接CD,首先求出AD,由△ACD∽△ADE,得到 ![]() ,即可求出AC解决问题.(3)作OF⊥MN于F,则四边形ODEF是矩形,根据tan∠CAB=
,即可求出AC解决问题.(3)作OF⊥MN于F,则四边形ODEF是矩形,根据tan∠CAB= ![]() ,求出AF即可解决问题.
,求出AF即可解决问题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目