题目内容
如下图，在矩形ABCD中，DE⊥AC于E，设∠ADE=α，且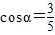
，AB=4，则AD的长为 ．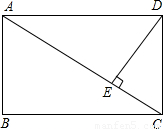
【答案】分析：根据等角的余角相等，得∠BAC=∠ADE=α；根据锐角三角函数定义可求AC的长，运用勾股定理求BC的长，即为AD的长．
解答：解：在△ABC与△AED中，
∵DE⊥AC于E，∠ABC=90°，
∠EAD=∠ACB，
∴∠BAC=∠ADE=α．
∴cos∠BAC=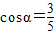
，
∴AC=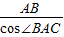
=
．
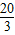∴BC=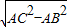
=
．
∴AD=BC=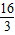
．
点评：此题综合运用了锐角三角函数的知识、勾股定理、矩形的性质．
解答：解：在△ABC与△AED中，
∵DE⊥AC于E，∠ABC=90°，
∠EAD=∠ACB，
∴∠BAC=∠ADE=α．
∴cos∠BAC=
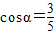，∴AC=
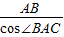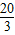=．∴BC=
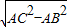=．∴AD=BC=
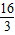．点评：此题综合运用了锐角三角函数的知识、勾股定理、矩形的性质．
练习册系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
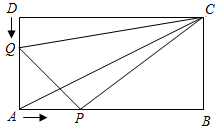如下图，在矩形ABCD中，AB=12cm，BC=6cm．点P沿AB边从点A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1 cm/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6）那么：
