��Ŀ����
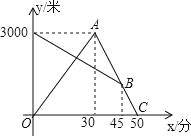
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�� ���������ᡱ ��ͼ�е�A��ʾ��11����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������29�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
�ʣ���1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��B���������������ij�����Q��O���������������ij�����ȣ�

���𰸡���1��19.5���룩����2��M����Ӧ����Ϊ5.��3��t��ֵΪ3��10.5��![]() ��18.
��18.
��������
��1��������߶�AO��OB��BC�ij���,�ֱ����������ʱ,��Ӽ���,
��2������ʱ����ͬ,A��B��·��֮�͵���ȫ��29����λ������ʽ���⼴��,
��3������PB��OQ���,�ɵ÷���,���ݷ��̼������.
��1����P�˶�����Cʱ������ʱ��t =11��2+10��1+8��2=19.5���룩��
��2�������֪��P��Q�����������߶�OB����M������OM=x.
��![]() +x=8+
+x=8+![]() ��
��
x=5 ��
M����Ӧ����Ϊ5.
��3��P��B���������������ij�����Q��O���������������ij��������5�ֿ��ܣ� �ٶ���P��AO�ϣ�����Q��CB�ϣ�����8-t=11-2t,�����t=3.
�ڶ���P��OB�ϣ�����Q��CB�ϣ�����8-t=(t-5.5)![]() ,�����t=6.75,������,��ʱ��P����OB�ϣ�
,�����t=6.75,������,��ʱ��P����OB�ϣ�
�۶���P��OB�ϣ�����Q��BO�ϣ�����(t-5.5)![]() 1=(t-8)
1=(t-8)![]() ,��ã�t=10.5.
,��ã�t=10.5.
�ܶ���P��OB�ϣ�����Q��OA�ϣ�����10-��t-5.5��![]() 1=t-13,�����t=
1=t-13,�����t=![]() ,
,
�ݶ���P��BC�ϣ�����Q��OA�ϣ�����10+2(t-15.5)=t-13+10,�����![]()
���ϣ�t��ֵΪ3��10.5��![]() ��18.
��18.

����Ŀ��ijУ��չ�ˡ�����ϲ������ʦ����ѡ���ȷ��������ѡ��������ѧ���ͽ�ʦ������4����ѡ��ʦ����ͶƱ��ÿƱѡ1����ѡ��ʦ��ÿλ��ѡ��ʦ�õ��Ľ�ʦƱ����5����ѧ��Ʊ���ĺ���Ϊ�ý�ʦ����Ʊ���������Ǹ���ѧ���ͽ�ʦ����ͶƱ������Ƶ�ͳ�Ʊ�������ͳ��ͼ������������ ѧ��ͶƱ���ͳ�Ʊ�
��ѡ��ʦ | ����ʦ | ����ʦ | ����ʦ | ����ʦ |
��Ʊ�� | 200 | 300 |
��1��������25λ��ʦ�����μ�ͶƱ��������ʦ�õ��Ľ�ʦƱ���Ƕ��٣��벹ȫ����ͳ��ͼ�������ڴ𰸾����Ӧ��ͼ�ϣ�
��2������ʦ������ʦ�õ���ѧ����Ʊ����600���Ҷ���ʦ�õ���ѧ��Ʊ��������ʦ�õ���ѧ��Ʊ����3����40Ʊ������ʦ������ʦ�õ���ѧ��Ʊ���ֱ��Ƕ��٣�
��3���ڣ�1������2���������£����ܵ�Ʊ���ϸߵ�2����ʦ��ѡ���в���������Ϊ��ѡ�����������λ��ʦ��Ϊʲô��