题目内容
如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD交于点O,且AO平分∠BAC。
(1)猜想OB与OC的数量关系,并说明理由.
(2)若∠BAC=60°,问△ADC经过怎样的变换能与△AEB重合?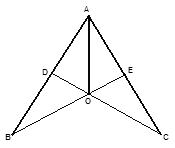
(1)猜想OB与OC的数量关系,并说明理由.
(2)若∠BAC=60°,问△ADC经过怎样的变换能与△AEB重合?

(1)猜想OB="OC"
先说明△AOD≌△AOE(AAS)得DO="OE"
再说明△BOD≌COE(ASA)得BO="CO"
(2)先将△ADC绕着点A,按逆时针方向旋转60°,再以AE所在的直线为对称轴作轴对称变换。(不唯一)
先说明△AOD≌△AOE(AAS)得DO="OE"
再说明△BOD≌COE(ASA)得BO="CO"
(2)先将△ADC绕着点A,按逆时针方向旋转60°,再以AE所在的直线为对称轴作轴对称变换。(不唯一)
(1)根据垂直定义可得∠ADC=∠AEB=90°,然后证明得到∠B=∠C,再根据角平分线定义可得∠BAO=∠CAO,然后利用“角角边”证明△ABO与△ACO全等,根据全等三角形对应边相等即可证明;
(2)根据轴对称图形的性质,△ADC与△AEB关于直线AO成轴对称.
(2)根据轴对称图形的性质,△ADC与△AEB关于直线AO成轴对称.

练习册系列答案
相关题目