��Ŀ����
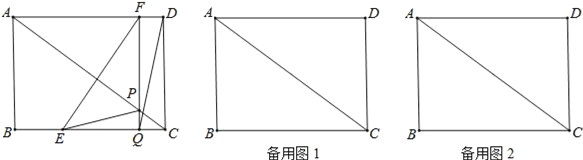
����Ŀ����ͼ���ھ���ABCD�У�AB=6cm��BC=8cm�������E�ɵ�B������BC�������C�����˶���ͬʱ��F�ɵ�D������DA�������A�����˶������ǵ��ٶȷֱ�Ϊ2cm/s��1cm/s��FQ��BC���ֱ�AC��BC�ڵ�P��Q�����˶�ʱ��Ϊt��s����0��t��4����
��1������EF��DQ�����ı���EQDFΪƽ���ı��Σ���t��ֵ��
��2������EP�����EPC�����Ϊycm2����y��t�ĺ�����ϵʽ������y�����ֵ��
��3������EPQ���ADC���ƣ���ֱ��д��t��ֵ��
���𰸡���1��t=2s����2��![]() ��3����3��2s��
��3����3��2s��![]() s��
s��![]() s��
s��
�����������������������ADC=��BCD=90����FQ��BC�ó��ı���FQCDΪ���Σ���CQ=DF=t��EQ=BC��BE=8��3t������ƽ���ı��ε����ʵã���t��ֵ������Rt��ABC�����ACB������ֵ��Ȼ���Rt��PQC����ACB������ֵ�ó�PQ�ij��ȣ�Ȼ��ó�y��t�ĺ�����ϵ�죬�����ֵ���������������Ƶó�t��ֵ��
�����������1���ھ���ABCD�У���ADC=��BCD=90������FQ��BC�����FQC=90�������ı���FQCDΪ���Σ�
��CQ=DF=t����EQ=BC-BE-CQ=8-2t-t=8-3t�� ���ı���EQDFΪƽ���ı��Σ� ��EQ=DF��
��t=8-3t�� ��t=2��s����
��2����Rt��ABC��tan��ACB=![]() �� ����Rt��PQC��tan��ACB=
�� ����Rt��PQC��tan��ACB=![]() �� ��PQ=
�� ��PQ=![]() ��
��
��![]() �� ��
�� ��![]() ����
����![]() �� ��y�����ֵΪ3��
�� ��y�����ֵΪ3��
��3������EPQ����ADC���ƣ�t��ֵΪ2s��![]() s��
s��![]() s��
s��
