��Ŀ����
����Ŀ������Rt��ABC�У���BAC=90������A����B�ֱ���x�ᡢy���������㣬ֱ�DZ�AC��x���ڵ�D��б��BC��y���ڵ�E��

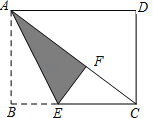
��1����ͼ��1������A��0��1����B��2��0������C������ꣻ
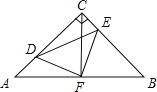
��2����ͼ��2����������Rt��ABC�˶���ʹ��DǡΪAC�е�ʱ������DE����֤����ADB=��CDE
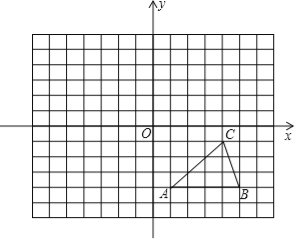
��3����ͼ��3�����ڵ���Rt��ABC�����˶��Ĺ����У�������BDʼ������ABC��ƽ���ߣ���̽�����߶�OA��OD��BD����֮���Ƿ����ijһ�̶���������ϵ����˵�����ɣ�
���𰸡���1��C����1����1������2������������3��BD=2��OA+OD����
��������
�����������1������C��CF��y���ڵ�Fͨ��֤��ACF�ա�ABO��CF=OA=1��AF=OB=2�����OF��ֵ���Ϳ������C�����ꣻ
��2������C��CG��AC��y���ڵ�G����֤����ACG�ա�ABD�Ϳ��Եó�CG=AD=CD����DCE=��GCE=45������֤����DCE�ա�GCE�Ϳ��Եó����ۣ�
��3����OB�Ͻ�ȡOH=OD������AH���ɶԳ��Ե�AD=AH����ADH=��AHD����֤��AHD=��ADH=��BAO=��BEO����֤����ACE�ա�BAH�Ϳ��Եó����ۣ�
��1���⣺����C��CF��y���ڵ�F��
���AFC=90����
���CAF+��ACF=90����
�ߡ�ABC�ǵ���ֱ�������Σ���BAC=90����
��AC=AB����CAF+��BAO=90������AFC=��BAC��
���ACF=��BAO��
����ACF����ABO��
 ��
��
���ACF�ա�ABO��AAS��
��CF=OA=1��AF=OB=2
��OF=1
��C����1����1����
��2��֤��������C��CG��AC��y���ڵ�G��
���ACG=��BAC=90����
���AGC+��GAC=90����
�ߡ�CAG+��BAO=90����
���AGC=��BAO��
�ߡ�ADO+��DAO=90������DAO+��BAO=90����
���ADO=��BAO��
���AGC=��ADO��
����ACG����ABD��

���ACG�ա�ABD��AAS����
��CG=AD=CD��
�ߡ�ACB=��ABC=45����
���DCE=��GCE=45����
����DCE����GCE��
 ��
��
���DCE�ա�GCE��SAS����
���CDE=��G��
���ADB=��CDE��
��3���⣺��OB�Ͻ�ȡOH=OD������AH
�ɶԳ��Ե�AD=AH����ADH=��AHD��
�ߡ�ADH=��BAO��
���BAO=��AHD��
��BD����ABC��ƽ���ߣ�
���ABO=��EBO��
�ߡ�AOB=��EOB=90����
����AOB����EOB��
 ��
��
���AOB�ա�EOB��ASA����
��AB=EB��AO=EO��
���BAO=��BEO��
���AHD=��ADH=��BAO=��BEO��
���AEC=��BHA��
����AEC����BHA��
 ��
��
���ACE�ա�BAH��AAS��
��AE=BH=2OA
��DH=2OD
��BD=2��OA+OD����




 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�