题目内容
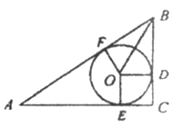
【题目】如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD的值为___________.
【答案】![]()
【解析】分析:首先根据切线的性质和切线长定理证得四边形OECD是正方形,那么AC+BC-AB即为2R(⊙O的半径R)的值,由此可得到OD、CD的值,进而可在Rt△OBD中求出∠OBD的正切值.
详解:∵BC、AC、AB都是⊙O的切线,
∴CD=CE、AE=AF、BF=BD,且OD⊥BC、OE⊥AC;
易证得四边形OECD是矩形,由OE=OD可证得四边形OECD是正方形;
设OD=OE=CD=R,则:AC+BC-AB=AE+R+BD+R-AF-BF=2R,
即R=![]() (AC+BC-AB)=1,
(AC+BC-AB)=1,
∴BD=BC-CD=3-1=2;
在Rt△OBD中,tan∠OBD=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目
【题目】某公司销售部有销售人员14人,为提高工作效率和员工的积极性,准备实行“每月定额销售,超额有奖”的措施.调查这14位销售人员某月的销售量,获得数据如下表:
月销售量(件) | 145 | 55 | 37 | 30 | 24 | 18 |
人数(人) | 1 | 1 | 2 | 5 | 3 | 2 |
(1)求这14位营销人员该月销售量的平均数和中位数
(2)如果你是该公司的销售部管理者,你将如何确定这个定额?请说明理由.