Question

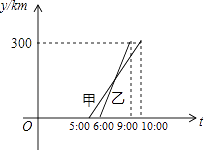
【题目】甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与t的对应关系如图所示：

（1）A、B两城之间距离是多少千米？
（2）求乙车出发多长时间追上甲车？
（3）直接写出甲车出发多长时间，两车相距20千米．

Answer 1

【答案】
（1）解：由图象可知A、B两城之间距离是300千米．
（2）解：设乙车出发x小时追上甲车．

由图象可知，甲的速度= =60千米/小时．

乙的速度= =75千米/小时．

由题意（75﹣60）x=60

解得x=4小时．

（3）解：设y甲=kx+b，则 解得 ，

∴y甲=60x﹣300，

设y乙=k′x+b′，则 ，解得 ，

∴y乙=100x﹣600，

∵两车相距20千米，

∴y甲﹣y乙=20或y乙﹣y甲=20或y甲=20或y甲=280，

即60x﹣300﹣（100x﹣600）=20或100x﹣600﹣（60x﹣300）=20或60x﹣300=20或60x﹣300=280

解得x=7或8或 或 ，

∵7﹣5=2，8﹣5=3， ﹣5= ， ﹣ 5=

∴甲车出发2小时或3小时或 小时或 小时，两车相距20千米．

【解析】解题的关键是学会利用函数解决实际问题，学会转化的思想，把问题转化为方程，属于中考常考题型．（1）根据图象即可得出结论．（2）先求出甲乙两人的速度，再列出方程即可解决问题．（3）根据y甲﹣y乙=20或y乙﹣y甲=20，列出方程即可解决．本题考查一次函数的应用、行程问题等知识，