��Ŀ����
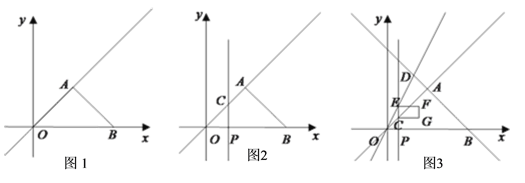
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�����ֱ�ǡ�AOB��б��OB��x�ϣ�����A������Ϊ��3��3��.
��1����ֱ��OA�Ľ���ʽ��
��2����ͼ2�������P��x���������ϵ�һ�����㣬����P��PC��y�ᣬ��ֱ��OA�ڵ�C�����P������Ϊ��m��0������A��C��P��BΪ������ı������ΪS����S��m֮��ĺ�����ϵʽ��
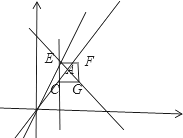
��3����ͼ3�������D��2��a����ֱ��AB��. ����O��D��ֱ��OD����ֱ��PC�ڵ�E����CE���Ҳ�������CGFE������CG=![]() �������CGFE���AOB�ص�����Ϊ��Գ�ͼ��ʱm��ȡֵ��Χ.
�������CGFE���AOB�ص�����Ϊ��Գ�ͼ��ʱm��ȡֵ��Χ.
���𰸡�
�������������������1����ֱ��OM�Ľ���ʽΪy=kx(k��0)������A��3��3����ֱ��OA�ϣ��õ�k=1����ֱ��OA�Ľ���ʽy=x��
��2������A��AM��x���ڵ�M����֪A������꣬�������M��3��0����B��6��0����P��m��0����C��m��m����������A��C��P��BΪ������ı��ε��������Ҫ��������ǣ���0��m��3ʱ����3��m��6ʱ����m��6ʱ����������3�������Ӱ���ֵ�������㷽�����������ͬ���Ա���ȡֵ��Χ�ڣ�S��m�ĺ�����ϵʽ��
��3�����ݵ���ֱ�������κ͵��������ε����ʣ��������m�ķ�Χ��
�����������1����ֱ��OA�Ľ���ʽΪy=kx��
��ֱ��OA������A��3��3����
��3=3k����� k=1��
��ֱ��OA�Ľ���ʽΪy=x��
��2������A��AM��x���ڵ�M��
��M��3��0����B��6��0����P��m��0����C��m��m����
��0��m��3ʱ�����ͼ����
��ͼ�� |
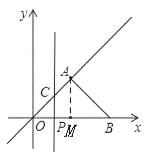
S=S��AOB��S��COP
=![]() AMOB��
AMOB��![]() OPPC
OPPC
=![]() ��
��
��3��m��6ʱ�����ͼ����
��ͼ�� |
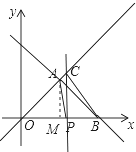
S=S��COB��S��AOP
=![]() PCOB��
PCOB��![]() OPAM
OPAM
=![]() ��
��
��m��6ʱ�����ͼ����
��ͼ�� |
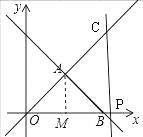
S=S��COP��S��AOB
=![]() PCOP��
PCOP��![]() OBAM
OBAM
=![]() ��
��
��3����C��ֱ��OA�ϣ�G��ֱ��AB��ʱ������CGFE����AOB�ص�����Ϊ��Գ�ͼ�Σ���ʱm=![]() ��
��
��m=3ʱC���A���غϣ������CGFE����AB���ص�����
����m��ȡֵ��Χʱ![]() ��m��3��
��m��3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�