题目内容
说说理由．已知线段a、b、c、d（b≠d），如果| a |
| b |
| c |
| d |
| a-c |
| b-d |
| a+c |
| b+d |
分析：根据比例的等比性质即可得出结果．
解答：解：如果
=
，那么
=
成立．理由如下：
设
=
=k，则
=
=k，
由等比性质得：
=k，
=k，
∴
=
．
故当
=
时，
=
．
| a |
| b |
| c |
| d |
| a-c |
| b-d |
| a+c |
| b+d |
设
| a |
| b |
| c |
| d |
| a |
| b |
| -c |
| -d |
由等比性质得：
| a-c |
| b-d |
| a+c |
| b+d |
∴
| a-c |
| b-d |
| a+c |
| b+d |
故当
| a |
| b |
| c |
| d |
| a-c |
| b-d |
| a+c |
| b+d |
点评：本题考查了等比性质：若
=
=…=
=k，那么
=k（b+d+…+n≠0）．
| a |
| b |
| c |
| d |
| m |
| n |
| a+c+…+m |
| b+d+…+n |
练习册系列答案
相关题目
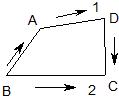23、如图，已知A，B，C，D四点．
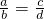，那么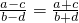
成立吗？为什么？