题目内容
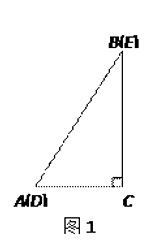
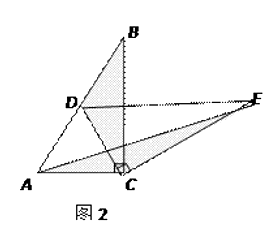
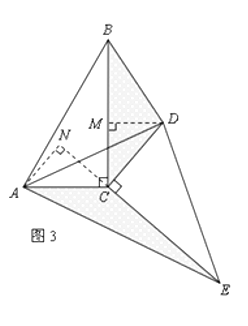
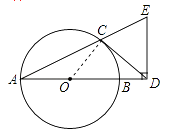
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB= ![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
【答案】
(1)证明:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,
∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,
∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE
(2)解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,
在Rt△EAD中,∵tan∠CAB= ![]() ,
,
∴ED= ![]() AD=
AD= ![]() (3+x),由(1)知,DC=
(3+x),由(1)知,DC= ![]() (3+x),
(3+x),
在Rt△OCD中, ![]() ,
,
则 ![]() ,
,
解得: ![]() (舍去),
(舍去), ![]() ,
,
故BD=1.
【解析】(1)抓住已知条件CD是⊙O的切线,因此连接OC得出∠OCD=90°,证得∠ACO+∠DCE=90°,再根据ED⊥AD,去证明∠EAD+∠E=90°,由OC=OA,得出∠ACO=∠EAD,根据等角的余角相等即可证得结论。
(2)设BD=x,由AB=3,求出OB的长,表示出OD的长,再在Rt△EAD中,由tan∠CAB的值,可表示出DE的长,即可得到DC的长,然后在Rt△OCD中,利用勾股定理建立关于x的方程,求解即可得出BD的长。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中,初二年级25名同学的成绩![]() 满分为10分
满分为10分![]() 统计如下:
统计如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,10
,10
![]() 分及以上为A级,
分及以上为A级,![]() 分为B级
分为B级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分为C级
分为C级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分以下为D级
分以下为D级![]() 请把下面表格补充完整;
请把下面表格补充完整;
等级 | A | B | C | D |
人数 | 4 | 8 |
![]() 级8位同学成绩的中位数是多少,众数是多少;
级8位同学成绩的中位数是多少,众数是多少;
![]() 若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?