题目内容
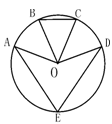
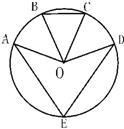
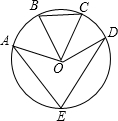 如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为
如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为
- A.138°
- B.46°
- C.69°
- D.92°
C
分析:欲求∠AED,又已知B、C分别是劣弧AD的三等分点,∠BOC=46°,可求∠AOD=138°,再利用圆周角与圆心角的关系求解.
解答:∵B、C分别是劣弧AD的三等分点,∠BOC=46°,
∴∠AOD=3×46°=138°,
∴∠AED= ∠AOD=138°÷2=69°(同弧所对的圆周角是所对的圆心角的一半).
∠AOD=138°÷2=69°(同弧所对的圆周角是所对的圆心角的一半).
故选C.
点评:本题考查了圆心角、弧、弦的关系以及圆周角定理.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
分析:欲求∠AED,又已知B、C分别是劣弧AD的三等分点,∠BOC=46°,可求∠AOD=138°,再利用圆周角与圆心角的关系求解.
解答:∵B、C分别是劣弧AD的三等分点,∠BOC=46°,
∴∠AOD=3×46°=138°,
∴∠AED=
 ∠AOD=138°÷2=69°(同弧所对的圆周角是所对的圆心角的一半).
∠AOD=138°÷2=69°(同弧所对的圆周角是所对的圆心角的一半).故选C.
点评:本题考查了圆心角、弧、弦的关系以及圆周角定理.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
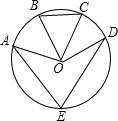 如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为( )
如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为( )| A、138° | B、46° | C、69° | D、92° |
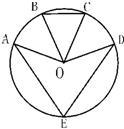 15、如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为
15、如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为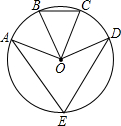 如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°.求∠AED的度数.
如图,已知点E是圆O上的点,B、C分别是劣弧AD的三等分点,∠BOC=46°.求∠AED的度数. 的三等分点,
的三等分点, 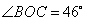 ,则
,则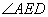 的度数为 .
的度数为 .